Question

After the exponential increase, population growth declines and stagnates. The growth curve is
A.S-shaped
B.J- shaped
C.Straight line
D.Circular

Answer 1

Hint:In nature, resources are limited. Therefore, the population growth in such habitat initially shows a lag phase, followed by a log and declining phase, reaching the carrying capacity. Such sigmoid shaped curves are called logistic growth curves.

Complete answer:In nature, populations do not have unlimited resources at their disposal. This leads to competition between individuals for limited resources. So, in nature exponential growth usually is not common.
Every natural habitat has fixed resources to support a population of individuals, beyond which no further increase in population can be supported. In a given habitat for that species, this is known as nature’s carrying capacity(K).
A population growing in a habitat with limited resources shows initially a lag phase (when individuals are maturing), and after that log phase when the population is proliferating and increasing in number and decrease (declining phase) and finally the population density reaches the carrying capacity (stationary phase, Asymptote). The graph results in a sigmoid curve. This type of population growth is called Verhulst- Pearl Logistic Growth.

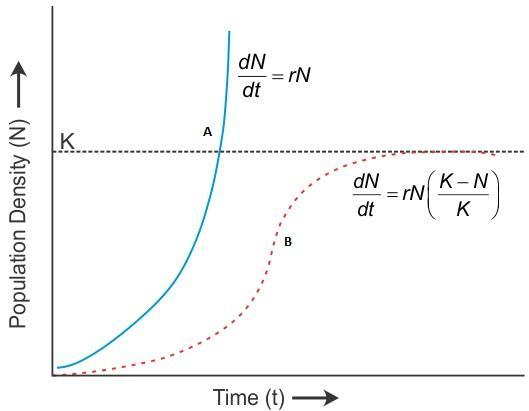
Where,
N = Population density at time t
r = intrinsic rate of natural increase
K = Carrying capacity
In the graph, A curve is the exponential growth curve.
In the graph, the B curve is the logistic curve.
The logistic growth curve is considered a more realistic one.
So, the answer is option A. S-shaped.

Note:When food and space for a population are unlimited, each species reproduces and then the population grows in an exponential ratio as stated by Darwin. When growing in unlimited resources, where there is no competition, the population of such species will reproduce exponentially and reach a large number in a short period. For such a population graph obtained is J- shaped.