Question

All congruent figures are similar, but the similar figures are not congruent. Is this statement true or false?
(a) False
(b) Both A and C
(c) True
(d) Not applicable

Answer 1

Hint: Concept of congruence and similarity between any two figures should be known. Congruence can be defined as “Both the figures are having the same shape, same size, everything to be equal”, whereas similarity means “same size, same ratios, same angle but different in size”.

Complete step-by-step answer:
Congruence basically means that two objects have the same size and shape. Although congruent objects are identical, their orientation and physical appearance will differ in 3D (3-dimensional) plane. It can be better understood by seeing the figure given below.

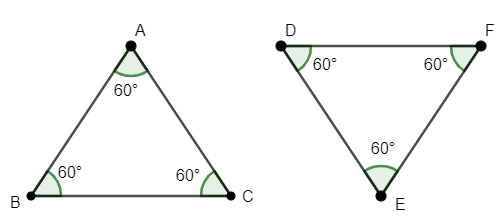
As we can see, the shape, size angle are the same in both triangles ABC and DEF but the triangle DEF is inverted compared to triangle ABC.
Now, talking about similarity, it is defined as two objects or figures having the same shape but not same size. For example, two circles will be the same in shape because they are circles but will be having different radius. Figure can be seen below for better understanding:

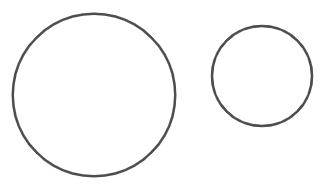
This both circles are considered to be similar but not congruent.
There are some rules to test similarity between 2 objects:
i. AA: If two angles are equal.
ii. SSS: If 3 corresponding sides are equal in ratio.
iii. SAS: If the ratio of two corresponding sides are equal and their included angle is equal.
Now, we are given the statement that “All congruent figures are similar, but the similar figures are not congruent” which is true by seeing the above explanation.
Hence, option (c) is the correct answer.

Note: Remember these above points because both are somewhat inter-related to each other. Also, there is slight variation in indicating congruence and similarity which is given by:
For congruent triangles: $\Delta ABC\cong \Delta DEF$
For similar triangles: $\Delta ABC\sim \Delta DEF$
So, don’t make mistakes considering congruency as similarity and vice-versa.