Question

Altitudes of a triangle are concurrent – prove by vector method.

Answer 1

Hint: To solve the question, we have to represent the information of sides and altitude of a triangle in vector form using basic principles of vectors. To prove that altitudes of a triangle are concurrent, we have to prove that the line segment joining the orthocentre and a vertex considering the altitudes drawn from the other two vertices of triangle meet at the orthocentre. To solve further, we have to apply the properties of the dot product to prove that the line segment joining the orthocentre and a vertex is perpendicular to the side of the triangle.

Complete step by step answer:
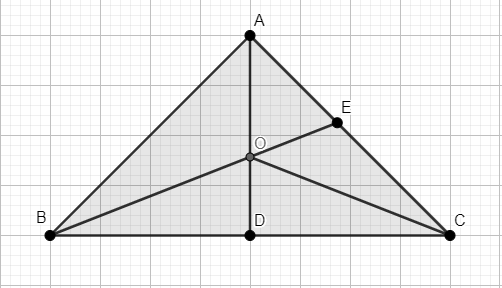
Let the given triangle be $$\mathrm{\Delta }ABC$$ with vertices A, B, C of position vectors respectively.
Let AD, BE be the altitudes of the given triangle.
Let O be the orthocentre of the given triangle of position vectors at origin.
We know that orthocentre is the point of intersection of the altitudes. Thus, O is the point of intersection of AD and BE.

The vector representation of OA = $$\overrightarrow{a}$$
The vector representation of OB = $$\overrightarrow{b}$$
The vector representation of OC = $$\overrightarrow{c}$$
We know that AD is perpendicular to BC, by the definition of an altitude of a triangle.
Thus, we get that OA is perpendicular to BC.
The vector representation of the above statement is
$$\overrightarrow{a}.(\overrightarrow{c}-\overrightarrow{b})=0$$
Since we know that the dot product of perpendicular vectors is 0.
By solving the above equation, we get
$$\overrightarrow{a}.\overrightarrow{c}-\overrightarrow{a}.\overrightarrow{b}=0$$ …… (1)
We know that BE is perpendicular to CA, by the definition of an altitude of a triangle.
Thus, we get that OB is perpendicular to CA.
The vector representation of the above statement is
$$\overrightarrow{b}.(\overrightarrow{a}-\overrightarrow{c})=0$$
$$\overrightarrow{a}.\overrightarrow{b}-\overrightarrow{c}.\overrightarrow{b}=0$$
By adding the above equation and equation (1), we get
$$\begin{array}{rl}& \overrightarrow{a}.\overrightarrow{b}-\overrightarrow{c}.\overrightarrow{b}+\overrightarrow{a}.\overrightarrow{c}-\overrightarrow{a}.\overrightarrow{b}=0+0\\ & \overrightarrow{a}.\overrightarrow{c}-\overrightarrow{c}.\overrightarrow{b}=0\\ & \overrightarrow{c}.(\overrightarrow{a}-\overrightarrow{b})=0\end{array}$$
Thus, we get OC is perpendicular to BA.
This implies OC is an altitude of the given triangle.
Thus, the altitudes of a triangle are concurrent.

Note: The possibility of mistake can be, not analysing that proving altitudes of a triangle are concurrent is equal to proving that the line segment joining the orthocentre and a vertex considering the altitudes drawn from the other two vertices of triangle meet at the orthocentre. The possibility of mistake can be not applying the properties of the dot product to prove that the line segment joining the orthocentre and a vertex is perpendicular to the side of the triangle.