
An
Answer
499.2k+ views
- Hint: The scattering of an alpha particle through a large angle with respect to its original direction of motion is caused by an atom whose most of the mass and all of the positive electric charge is being concentrated at the center or the nucleus of the atom. In this collision between the alpha particle and the atom, we define a term known as distance of closest approach, which is the distance between the centres of the alpha particle and the atom. At the distance of closest approach, the kinetic energy of the alpha particle is converted into its potential energy.
Complete step-by-step solution
The distance of the closest approach of two particles is defined as the distance between their centers when the particles are externally tangent to each other. The objects can be exact geometric shapes or physical particles with well-defined boundaries. The distance of closest approach is also called the contact distance.
For the simplest objects, such as spheres, the distance of closest approach is the sum of their radii. For non-spherical objects, the distance of closest approach is a function of the orientation of the objects in the space.
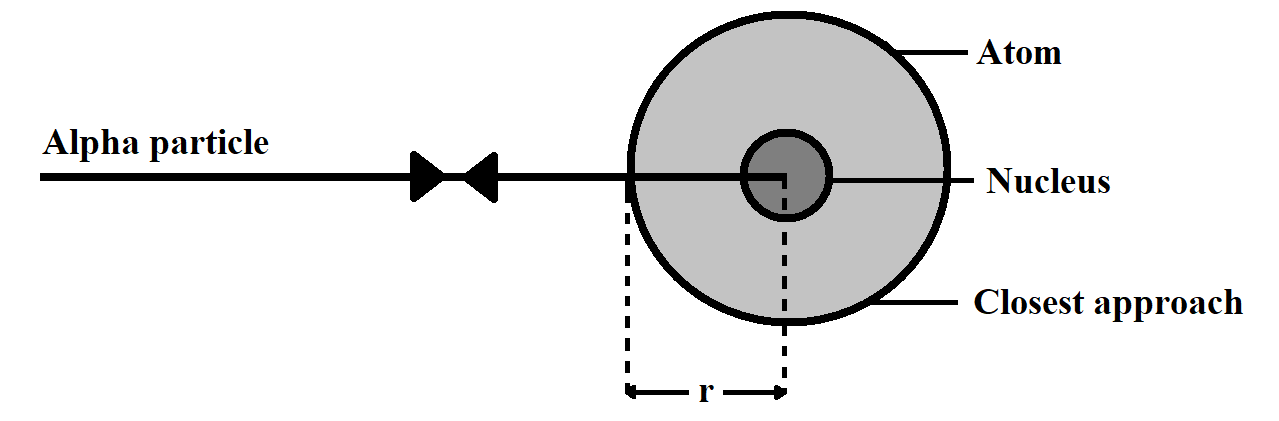
At the distance of closest approach, the whole kinetic energy of the particle gets converted into potential energy.
Therefore,
Where,
Putting values,
We get,
The distance of closest approach is
Hence, the correct option is D.
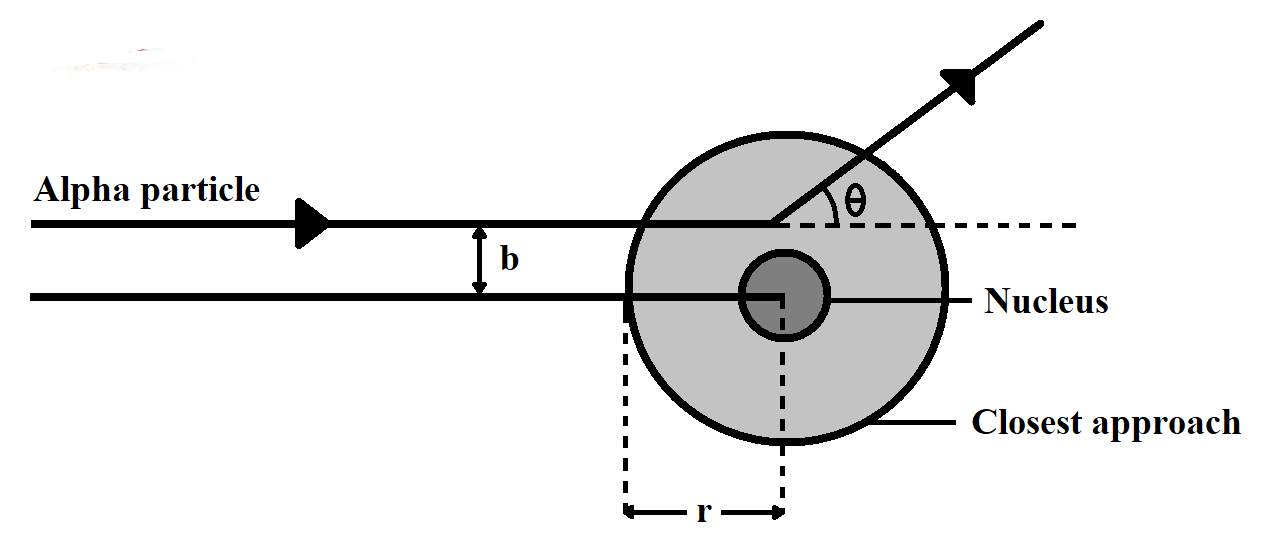
Note: Students should note the key difference between the distance of closest approach and the impact meter. Distance of closest approach is the distance between the centre of nucleus and the point from which the alpha particle, which is approaching directly to the nucleus, returns, while Impact parameter is expressed as the perpendicular distance of the velocity vector of the alpha particle from the central line of the nucleus; when the particle is far away from the atom.
Distance of closest approach is expressed as
Complete step-by-step solution
The distance of the closest approach of two particles is defined as the distance between their centers when the particles are externally tangent to each other. The objects can be exact geometric shapes or physical particles with well-defined boundaries. The distance of closest approach is also called the contact distance.
For the simplest objects, such as spheres, the distance of closest approach is the sum of their radii. For non-spherical objects, the distance of closest approach is a function of the orientation of the objects in the space.

At the distance of closest approach, the whole kinetic energy of the particle gets converted into potential energy.
Therefore,
Where,
Putting values,
We get,
The distance of closest approach is
Hence, the correct option is D.
Note: Students should note the key difference between the distance of closest approach and the impact meter. Distance of closest approach is the distance between the centre of nucleus and the point from which the alpha particle, which is approaching directly to the nucleus, returns, while Impact parameter is expressed as the perpendicular distance of the velocity vector of the alpha particle from the central line of the nucleus; when the particle is far away from the atom.
Distance of closest approach is expressed as

Recently Updated Pages
Master Class 4 Maths: Engaging Questions & Answers for Success

Master Class 4 English: Engaging Questions & Answers for Success

Master Class 4 Science: Engaging Questions & Answers for Success

Class 4 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Trending doubts
What is the difference between resemblance and sem class 12 social science CBSE

What is the Full Form of PVC, PET, HDPE, LDPE, PP and PS ?

Draw ray diagrams each showing i myopic eye and ii class 12 physics CBSE

Why do the transition elements have higher enthalpies class 12 chemistry CBSE

What are the advantages of parallel combination over class 12 physics CBSE

What are the causes of overloading class 12 physics CBSE




