
An annular disk has an inner and outer radius
A)
B)
C)
D)
Answer
494.4k+ views
Hint: Here we have to imagine a hypothetical ring of radius X and thickness dx, the hypothetical ring is inside the ring. We have to find the electric field of the hypothetical ring first and then we have to integrate the electric field to get the electric field of the real ring on the point p on the y-axis.
Formula used:
The formula for finding out the coefficient of performance is given below.
Here,
The formula for charge on the hypothetical ring is
dq =
Complete step by step answer:
Step 1: Look at the below picture. Here, apart from the Big ring whose radius is
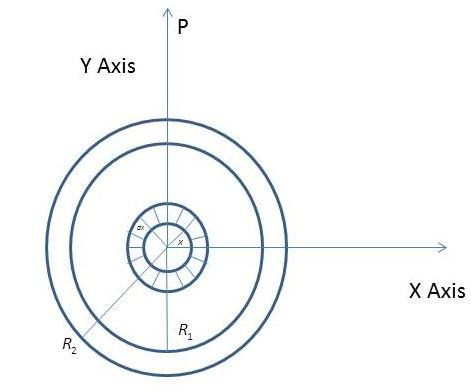
The charge on the hypothetical ring is
dq =
Now, we know the electric field due to a ring, which is
So, for a small charge dq, the equation becomes,
Put the value of dq in the above equation
Step 2: Calculating the total electric field of the ring by integrating the equation.
After solving the above equation we get
Now, we integrate the equation from
Let
Now differentiate
Differentiate each variable,
Here
Here, we have established a relation between xdx and pdp.
Now, put
Write the above equation in terms of
solving the above equation,
Simplify the above equation
Solving integration,
Simplify further,
Put the value of p i.e. p =
Put the upper limit (
The electric field at any point distant y along the axis of the disk is
Note:
The equation
Formula used:
The formula for finding out the coefficient of performance is given below.
Here,
The formula for charge on the hypothetical ring is
dq =
Complete step by step answer:
Step 1: Look at the below picture. Here, apart from the Big ring whose radius is

The charge on the hypothetical ring is
dq =
Now, we know the electric field due to a ring, which is
So, for a small charge dq, the equation becomes,
Put the value of dq in the above equation
Step 2: Calculating the total electric field of the ring by integrating the equation.
After solving the above equation we get
Now, we integrate the equation from
Let
Now differentiate
Differentiate each variable,
Here
Here, we have established a relation between xdx and pdp.
Now, put
Write the above equation in terms of
solving the above equation,
Simplify the above equation
Solving integration,
Simplify further,
Put the value of p i.e. p =
Put the upper limit (
The electric field at any point distant y along the axis of the disk is
Note:
The equation
Recently Updated Pages
Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Write the following in Roman numerals 25819 class 7 maths CBSE

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Write the differences between monocot plants and dicot class 11 biology CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light




