Question

An empty vessel is filled partially with water natural frequency
(A) Increase
(B) Decrease
(C) Remains unchanged
(D) Insufficient data

Answer 1

Hint: When the shape of the empty vessel is observed it is found that it looks like a cylinder. In comparison we can observe that it resembles a cylindrical organ pipe which is a musical instrument that is closed at one end. The following problem can be solved by using the properties of organ pipes.

Complete step by step solution:
An organ pipe is a musical instrument which consists of an air column with different depth which when blown by mouth or by pressurized air produces music that resonates at different frequencies which results in a different pitch. Pitch is a quality of sound that shows the degree of lowness and highness of tone which can be obtained by the rate of different vibrations.
The fundamental frequency of an organ pipe with one end closed can be given as
$ \Rightarrow f = \dfrac{v}{{4L}}$ ---------------- Equation $(1)$
Where $v = $velocity of sound that is entering the air column
$ \Rightarrow L = $Length of the air column
As an empty vessel resembles to organ pipe hence its fundamental frequency will be also given by the equation $(1)$
$ \Rightarrow {f_{vessel}} = \dfrac{v}{{4{L_{vessel}}}}$
Now it can be seen that here the frequency $f$ is inversely proportional to the Length $L$
$ \Rightarrow {f_{vessel}} \propto \dfrac{1}{{{L_{vessel}}}}$
As we are filling the vessel with water then the length of the air column of the vessel decreases as water will reflect the sound when blown into the vessel.

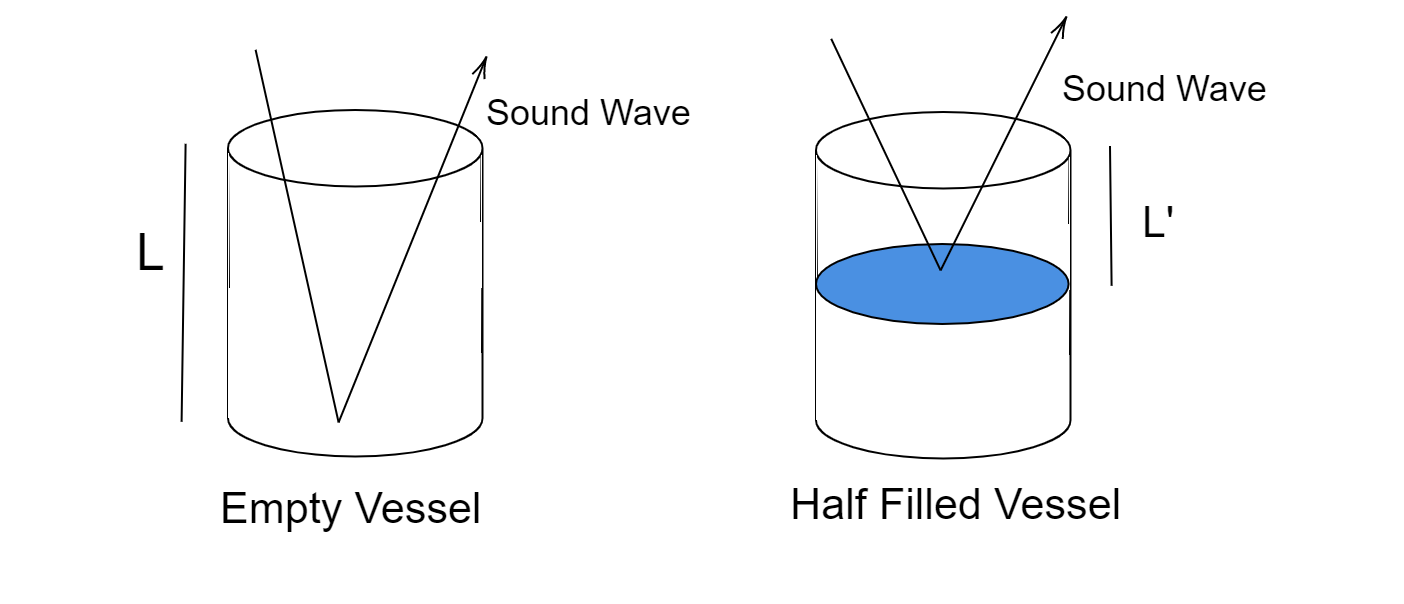
As the length of the air column decreases the frequency will increase because the frequency is inversely proportional to the length of the air column.

Hence option (A) is the correct answer.

Note: Here we have used the formula for the fundamental frequency of the organ pipe with one end closed but if both ends are open then the fundamental frequency of the organ pipe will be different than what is used in this problem. The fundamental frequency of the organ pipe with both ends open can be given by$f = \dfrac{v}{{2L}}$.