Question

An enemy plane is flying horizontally at an attitude of $2 km$ with a speed of $300 m{s^{ - 1}}.$ An army man with an anti-craft gun on the ground fires a shell with speed of $600 m{s^{ - 1}},$when the enemy plane is directly overhead. At what angle from the vertical should the gun be fired so as to hit the plane?
\[
A.\;{\text{90}}^\circ \\
B.\;6{\text{0}}^\circ \\
C.\;45^\circ \\
D.\;3{\text{0}}^\circ \\
\]

Answer 1

Hint:First,calculate distance travelled by using the given terms such as velocity. Here, distance travelled by the plane and the shell fired are the same. So equate them to get the required distance and then find the value of the angle made by the man to fire.

Complete step by step answer:
Let us draw the figure, to understand quickly and properly,

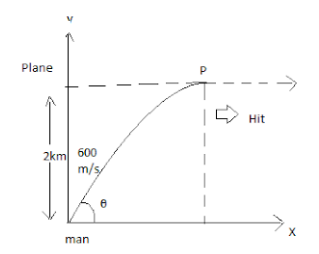
Velocity of the plane, $v = 300m/s$
Let initial angle at which man fires is $ = \theta $
Let P be the point at which it hit an enemy plane.
Initial speed of the fire shell, $v = 600m/s$
Elevation is given at $2km$
Let “t” be the time at which it hit,
Therefore distance travelled by plane in the horizontal direction$ = 300 \times t$ ....... (a)
Shell travelled in the x-direction =$ = 600 \times \cos \theta \times t$ ........ (b)
Now, equation (a) and (b) are equal as they travel the equal distance.
$300 \times t = 600 \times \cos \theta \times t$
Simplify the above equation –
Take “t” common from both the sides of the equation and remove them.
$300 = 600\cos \theta $
Make unknown angle the subject –
$
\cos \theta = \dfrac{{300}}{{600}} \\
\Rightarrow \cos \theta = \dfrac{1}{2} \\
\Rightarrow \theta = {\cos ^{ - 1}}\left( {\dfrac{1}{2}} \right) \\
\Rightarrow \theta = 60^\circ \\
 $
It makes angle, $\theta = 60^\circ $therefore, vertical angle is $ = 90^\circ - \theta = 90^\circ - 60^\circ = 30^\circ $
Therefore, the required answer is - The gun should be fired at an angle $30^\circ $ from the vertical so as to hit the plane.
Hence, from the given multiple choices – option D is the correct answer.

Note:Remember all the different trigonometric angles which are the angles given by the ratios of the trigonometric functions. The most important trigonometric angles are $0^\circ ,{\text{ 3}}0^\circ ,\;45^\circ ,{\text{ 6}}0^\circ {\text{ and 9}}0^\circ $. Remember the values of these angles for quick substitution for further simplification.