Question

An equilateral triangle has ______ lines of symmetry.
(a) 0
(b) 1
(c) 3
(d) 2

Answer 1

Hint: Draw a rough diagram of an equilateral triangle and check its different properties. Find out how many such lines can be drawn that can cut the triangle into two equal halves. The number of such lines will be the number of lines of symmetry and our answer.

Complete step by step answer:
Here, we have been asked to find the number of lines of symmetry that an equilateral triangle has. But first, we need to understand the term ‘lines of symmetry’.
In geometry, a geometric shape or object is symmetric if it can be divided into two or more identical pieces. There are certain types of symmetry like - reflectional symmetry, rotational symmetry, translational symmetry, etc. but here out main focus is on reflectional symmetry.
An object has reflectional symmetry if there is a line going through it that can divide it into two pieces that are mirror images of each other. Reflectional symmetry is also called the line or mirror symmetry.
Now, let us come to the question. We have an equilateral triangle.

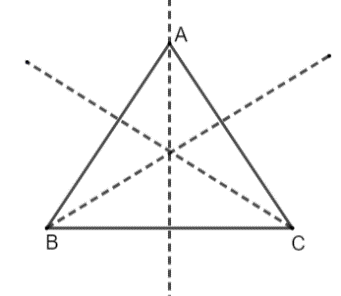
In the above figure clearly, we can see that we can draw three lines that can divide the equilateral triangle into two equal halves. The first line is drawn from vertex A passing through the side BC, the second line is drawn from vertex B passing through the side A, the third line is drawn from vertex C passing through the side AB. Therefore, an equilateral triangle has 3 lines of symmetry.
Hence, option (c) is the correct answer.

Note:
 One may note that the definition of lines of symmetry must be remembered to solve the question. In the topic ‘types of symmetry’ generally, questions are asked from the parts ‘line symmetry’ and ‘rotational symmetry’ in mathematics. So, these two types of symmetry must be memorized. Never forget to draw the figure of the shape asked otherwise you will get confused while imagining the lines of symmetry.