Question

An $fcc$ lattice has a lattice parameter \[a\] equal to $400pm$. Calculate the molar volume (in ML) of the lattice including all the empty space.
A. $10.8$
B. $96.2$
C. $8.6$
D. $9.6$

Answer 1

Hint: The ordered structure that has occurred from the intrinsic nature of the constituent particles or atoms to form symmetric patterns of the crystal structure that will repeat along all the dimensions are known as a unit cell. The numerous unit cells together form a crystal lattice. Each lattice point is being occupied by one particle or atom.

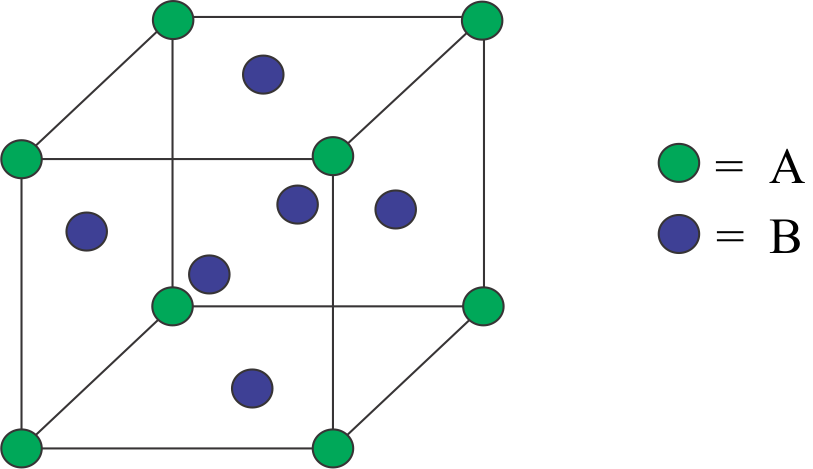
Complete step by step answer: The \[fcc\]unit cell is also known as the face centred cubic unit cell. This unit cell contains atoms at all the corners of the crystal lattice and at the centre of the faces of all the walls of the cube.
The corner atoms are being shared by eight more-unit cells. Thus, the contribution of each corner atom to a one-unit cell $fcc$ structure is $\dfrac{1}{8}$. And since, there are total eight corner atoms, therefore the contribution of all the corner atoms would be $\dfrac{1}{8} \times 8 = 1atom$
Similarly, the face atoms are being mutually shared by two-unit cells thus we can say that the contribution of each face atom would be \[\dfrac{1}{2}\]. Since, there are total six face atom, so the total contribution of face atoms would be $\dfrac{1}{2} \times 6 = 3atoms$
Therefore, we can say that the $fcc$ structure unit cell has $\left( {1 + 3 = 4} \right)4atoms$ in its structure.
Now, if an $fcc$ lattice has a lattice parameter $'a'$ equal to $400pm$, then
Volume of the unit cell = ${400^3}$
$\left[ {volume = {{\left( {side} \right)}^3}} \right]$
$ = 64 \times {10^{ - 24}}c{m^3}$
Volume of ${N_A}$ unit cell = $64 \times {10^{ - 24}} \times 6 \times {10^{23}}$ $\left[ {{N_A} = Avogadra{\text{ }}Number} \right]$
$ = 38.4c{m^3}$
Molar volume =$\dfrac{{38.4}}{4} = 9.6c{m^3}/mol$
Hence, the answer is option (D).

Note: On the basis of arrangements of atoms in space there can be different types of lattice structures. Mainly lattice structure can be fcc, bcc and hcp. In $fcc$ lattice structure, the coordination number is $12$ and the packing efficiency is $74\% $.