
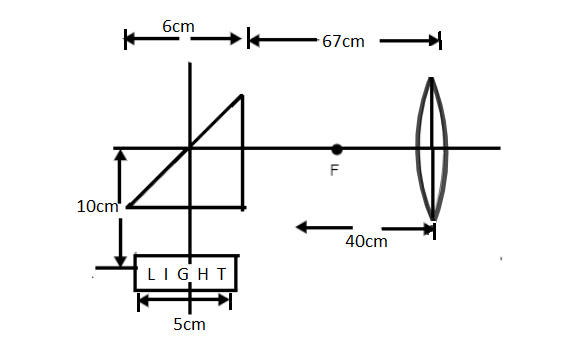
An isosceles right-angled prism and a convex lens (focal length = 40cm) are placed as shown in the figure, and a 5cm wide strip with the letter LIGHT written on it placed as indicated. What is the nature and the position of the image formed after the refraction through the prism and the lens? (Given the critical angle of the glass used for the prism and the lens is

Answer
476.4k+ views
Hint: In order to solve this question we will use simple rules of the image formation by prism then this image will act as an object for the convex lens and by using formula for the convex lens we will get an image formed by a combination of prism and the convex lens.
Formula used:
Complete step by step solution:
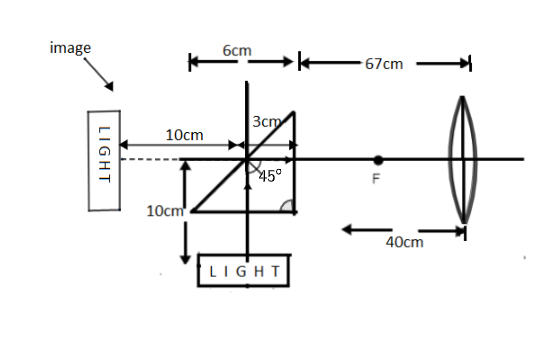
First we will see how and where the image is formed by the isosceles right-angled prism.
It is given in the question that the critical angle of the glass used for the prism is
From the figure we can see that the angle of the incident is
Therefore the rays that are coming from an object written as the LIGHT will fully reflect and form a virtual image with the same size of an object as shown in the figure.
Now this image will act as an object for the convex lens.
Distance of this image from the convex lens which will be call as object distance,
Here we will take object distance negative 80cm for convex lens.
Focal length is given as,
f = 40cm
Formula for the convex lens is,
Where, f = focal length
v = image distance
u = object distance.
Now substitute all the values in the formula.
Therefore the image formed by this combination is real, inverted and the same size.
Note:
When we are forming an image from the prism do not forget to consider 10cm distance because it can be mistaken as image formed on prism and we can misjudge object distance u as 67 + 3 which is 70cm which can give us wrong solution.
Formula used:
Complete step by step solution:

First we will see how and where the image is formed by the isosceles right-angled prism.
It is given in the question that the critical angle of the glass used for the prism is
From the figure we can see that the angle of the incident is
Therefore the rays that are coming from an object written as the LIGHT will fully reflect and form a virtual image with the same size of an object as shown in the figure.
Now this image will act as an object for the convex lens.
Distance of this image from the convex lens which will be call as object distance,
Here we will take object distance negative 80cm for convex lens.
Focal length is given as,
f = 40cm
Formula for the convex lens is,
Where, f = focal length
v = image distance
u = object distance.
Now substitute all the values in the formula.
Therefore the image formed by this combination is real, inverted and the same size.
Note:
When we are forming an image from the prism do not forget to consider 10cm distance because it can be mistaken as image formed on prism and we can misjudge object distance u as 67 + 3 which is 70cm which can give us wrong solution.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Class 12 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Trending doubts
Draw a labelled sketch of the human eye class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Which one of the following is a true fish A Jellyfish class 12 biology CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Write the difference between solid liquid and gas class 12 chemistry CBSE




