Answer
Verified401.5k+ views
Hint: We have given the length of two sides as 12 cm so let us assume that the third side be x then take the sum of two sides of length 12 cm and the third side x and equate it to 30. From this we will get the third side. To find the area of the triangle, use the Heron’s formula which is equal to $\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}$ where “s” is the semi perimeter and a, b and c are the sides of the triangle.
Complete step-by-step answer:
In the below diagram, we have shown an isosceles triangle ABC with AB = AC = 12 cm.
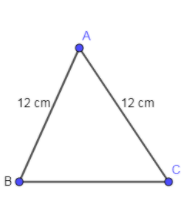
Let us assume that the length of the side BC is equal to x. We know that the perimeter of a triangle is the sum of all the sides of the triangle.
Perimeter of the triangle is equal to addition of AB, BC and CA. Adding all the three sides of the triangle we get,
$12+12+x$
It is given that the perimeter of the triangle is equal to 30 cm so equating the above expression we get,
$\begin{align}
& 12+12+x=30 \\
& \Rightarrow 24+x=30 \\
& \Rightarrow x=6cm \\
\end{align}$
From the above, we have got the length of the third side as 6 cm.
We are asked to find the area of the triangle. For that we are going to use the Heron’s formula which states that:
We are denoting the area of the triangle as $\Delta $.
$\Delta =\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}$
In the above formula, “s” represents the semi – perimeter of the triangle, “a, b and c” represents the sides of the triangle ABC.
Perimeter of the triangle is given as 30 cm so the semi perimeter is equal to half of the perimeter i.e. 15 cm.
We are taking $a=b=12cm$ and $c=6cm$ and the value of “s” as 15 cm. Substituting these values in Heron’s formula we get,
$\begin{align}
& \Delta =\sqrt{15\left( 15-12 \right)\left( 15-12 \right)\left( 15-6 \right)} \\
& \Rightarrow \Delta =\sqrt{15\left( 3 \right)\left( 3 \right)\left( 9 \right)} \\
& \Rightarrow \Delta =\sqrt{15{{\left( 3 \right)}^{4}}} \\
& \Rightarrow \Delta =9\sqrt{15} \\
\end{align}$
Hence, the area of the triangle is equal to $9\sqrt{15}c{{m}^{2}}$.
Note: The most common mistake that could happen in this problem is the calculation mistake. There is a trick to remember this Heron’s area formula.
$\Delta =\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}$
The trick is that remembering root over is easy but then you might forget what is inside the root over which you can remember like first all no side is subtracting from the semi perimeter $\left( s-0 \right)$ then side a has subtracted $\left( s-a \right)$ followed by side b $\left( s-b \right)$ then side c $\left( s-c \right)$.
Complete step-by-step answer:
In the below diagram, we have shown an isosceles triangle ABC with AB = AC = 12 cm.
Let us assume that the length of the side BC is equal to x. We know that the perimeter of a triangle is the sum of all the sides of the triangle.
Perimeter of the triangle is equal to addition of AB, BC and CA. Adding all the three sides of the triangle we get,
$12+12+x$
It is given that the perimeter of the triangle is equal to 30 cm so equating the above expression we get,
$\begin{align}
& 12+12+x=30 \\
& \Rightarrow 24+x=30 \\
& \Rightarrow x=6cm \\
\end{align}$
From the above, we have got the length of the third side as 6 cm.
We are asked to find the area of the triangle. For that we are going to use the Heron’s formula which states that:
We are denoting the area of the triangle as $\Delta $.
$\Delta =\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}$
In the above formula, “s” represents the semi – perimeter of the triangle, “a, b and c” represents the sides of the triangle ABC.
Perimeter of the triangle is given as 30 cm so the semi perimeter is equal to half of the perimeter i.e. 15 cm.
We are taking $a=b=12cm$ and $c=6cm$ and the value of “s” as 15 cm. Substituting these values in Heron’s formula we get,
$\begin{align}
& \Delta =\sqrt{15\left( 15-12 \right)\left( 15-12 \right)\left( 15-6 \right)} \\
& \Rightarrow \Delta =\sqrt{15\left( 3 \right)\left( 3 \right)\left( 9 \right)} \\
& \Rightarrow \Delta =\sqrt{15{{\left( 3 \right)}^{4}}} \\
& \Rightarrow \Delta =9\sqrt{15} \\
\end{align}$
Hence, the area of the triangle is equal to $9\sqrt{15}c{{m}^{2}}$.
Note: The most common mistake that could happen in this problem is the calculation mistake. There is a trick to remember this Heron’s area formula.
$\Delta =\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}$
The trick is that remembering root over is easy but then you might forget what is inside the root over which you can remember like first all no side is subtracting from the semi perimeter $\left( s-0 \right)$ then side a has subtracted $\left( s-a \right)$ followed by side b $\left( s-b \right)$ then side c $\left( s-c \right)$.