
An object is placed at a distance of 15 cm from a convex lens of focal length 20 cm. List four characteristics (nature, position etc.) of the image formed by the lens.
Answer
508.5k+ views
2 likes
Hint: To deal with this problem first, we need to find the distance of the image with the aid of the specified object distance and focal length using different lens formulas, then we will proceed further by observing the image formed by the lens.
Formula Used:
Complete step-by-step answer:
Here given that object distance u = -15 cm
(We assigned negative signs to object size, as we use the Cartesian lens and mirror system)
And focal length f = 20 cm
We know lens formula, which is given as
Substituting the value of u, f in this formula, we obtain
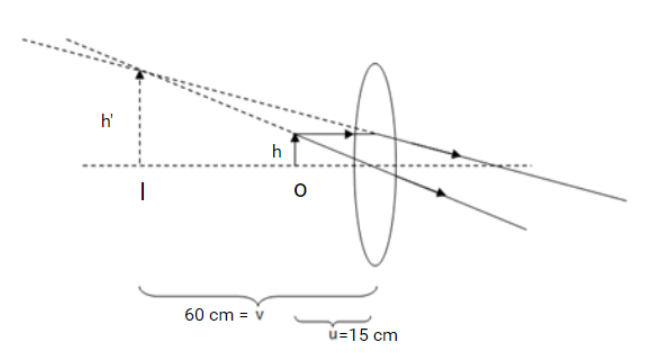
The picture distance from the lens is therefore 60 cm and the left side of the lens as an object would be left.
Referring from image
I refer to image and O refers to object , h’ and h refers to the height of image and object respectively.
And we know
Since m>1, which means enlarged and erect image.
The image formed by the lens has four features:
1. Image formed is virtual.
2. Image is erect.
3. Image is formed on the same side of the lens as the object.
4. Enlarged image.
Note: The lens formula applies to all situations with suitable conventions on signs. The formula for this lens applies to both concave and convex lenses. If the equation shows a negative image distance, then the image is a virtual image on the same side of the lens as the object. If this equation indicates a negative focal length, then the lens is not the converging lens but a diverging lens. Use this equation to locate image distance for either real or virtual image.
Formula Used:
Complete step-by-step answer:
Here given that object distance u = -15 cm
(We assigned negative signs to object size, as we use the Cartesian lens and mirror system)
And focal length f = 20 cm
We know lens formula, which is given as
Substituting the value of u, f in this formula, we obtain
The picture distance from the lens is therefore 60 cm and the left side of the lens as an object would be left.
Referring from image
I refer to image and O refers to object , h’ and h refers to the height of image and object respectively.
And we know
Since m>1, which means enlarged and erect image.

The image formed by the lens has four features:
1. Image formed is virtual.
2. Image is erect.
3. Image is formed on the same side of the lens as the object.
4. Enlarged image.
Note: The lens formula applies to all situations with suitable conventions on signs. The formula for this lens applies to both concave and convex lenses. If the equation shows a negative image distance, then the image is a virtual image on the same side of the lens as the object. If this equation indicates a negative focal length, then the lens is not the converging lens but a diverging lens. Use this equation to locate image distance for either real or virtual image.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Class 12 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Trending doubts
Draw a labelled sketch of the human eye class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Which one of the following is a true fish A Jellyfish class 12 biology CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Write the difference between solid liquid and gas class 12 chemistry CBSE




