Question

An object is placed at a distance of 30 cm from a concave lens of focal length 30 cm.
i. Use lens formula to determine the distance of the image from the lens.
ii. List four characteristics of the image (nature, position, size, erect/inverted) in this case.
iii. Draw a well labelled diagram to justify your answer part (ii)

Answer 1

Hint: Concave lenses are diverging lenses. The image formed by this lens is virtual upright and reduced in size. If the object is kept at the focus of the lens, then an image is produced in between the focus and the center of the lens.

Formula Used:
Lens Formula:
$\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$
where f is the focal length of the concave lens, v is the image distance from optical center, u is the object distance from optical center

Complete step by step answer:
A concave lens is a diverging lens. Unlike converging lenses, the images formed by the concave lens are always located on the side of the object, virtual, upright and smaller in size than the object.

Given:
Focal length of the concave lens: $f = 30cm$
Object distance from optical centre O: $u = 30cm$
From lens formula we know that:
$\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$
where f is the focal length of the concave lens, v is the image distance from optical center, u is the object distance from optical center

$\eqalign{
  & \Rightarrow \dfrac{1}{v} = \dfrac{1}{f} + \dfrac{1}{u} \cr
  & \Rightarrow \dfrac{1}{v} = \dfrac{1}{{ - 30}} + \dfrac{1}{{ - 30}}{\text{ }}\left[ {{\text{Substituting values of }}u{\text{ and }}f} \right] \cr
  & \Rightarrow \dfrac{1}{v} = \dfrac{{1 + 1}}{{ - 30}} \cr
  & \Rightarrow \dfrac{1}{v} = \dfrac{2}{{ - 30}} \cr
  & \therefore v = \dfrac{{ - 30}}{2} = - 15cm \cr} $
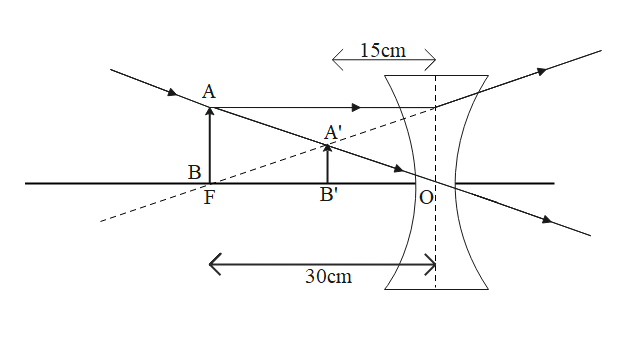
So, the image is produced at 15 cm from the lens’ optical centre.
The characteristics of the image formed by this concave lens are as follows:
   Virtual
   Erect
   Diminished
   The image is formed between the Optical center O and the focus F of the lens.
   It is 15 cm from the optical center O and is one the same side as the object itself.

The following diagram shows the image formed by a concave lens when the object is placed at its focus:

Note: The diverging property of a concave lens is very useful. Concave lenses are used to treat the disease of near-sightedness or myopia by using them in the lens of glasses. They are also used in cameras to reduce the chromatic aberrations caused by the convex lens.