Question

An oil funnel made of tin sheet consists of a 10cm long cylindrical portion attached to a frustum of a cone. If the total height is 22cm, diameter of the cylindrical portion is 8cm and the diameter of the top of the funnel is 18cm, find the area of the tin sheet required to make the funnel.

Answer 1

Hint: We see that the surface area required to make a tin sheet of funnel is the sum of curved surface area of the cylinder and frustum cone. We find curved surface area of the cylinder using the formula ${{A}_{1}}=2\pi rh$ and the curved surface area of the cylinder of frustum cone using the formula ${{A}_{2}}=\pi \left( {{r}_{1}}+{{r}_{2}} \right)l$ . We add ${{A}_{1}},{{A}_{2}}$ to get the answer. \[\]

Complete step by step answer:

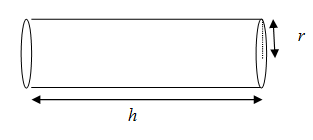
We know that the curved surface area of cylinder with radius at the edge $r$ and length $h$ is given by ${{A}_{1}}=2\pi rh$\[\]
 

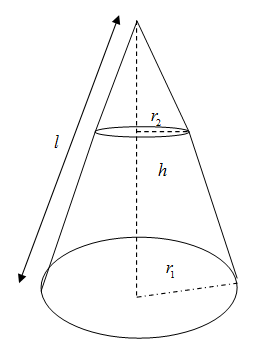
A frustum cone is lower part of a cone when a plane parallel to the base cuts the upper part We also know the curved surface area of frustum cone with radius of the base ${{r}_{1}}$, radius of the circular upper section ${{r}_{2}}$ and the slant height $l$ is given by ${{A}_{2}}=\pi \left( {{r}_{1}}+{{r}_{2}} \right)l$ . We can find slant height from ${{r}_{1}},{{r}_{2}},h$ by the formula $l=\sqrt{{{h}^{2}}+{{\left( {{r}_{1}}-{{r}_{2}} \right)}^{2}}}$\[\]

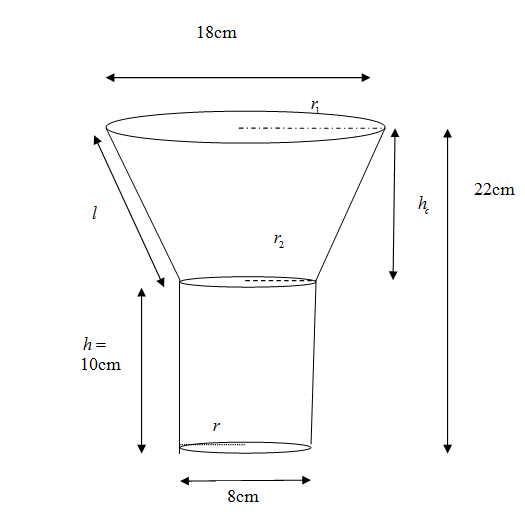
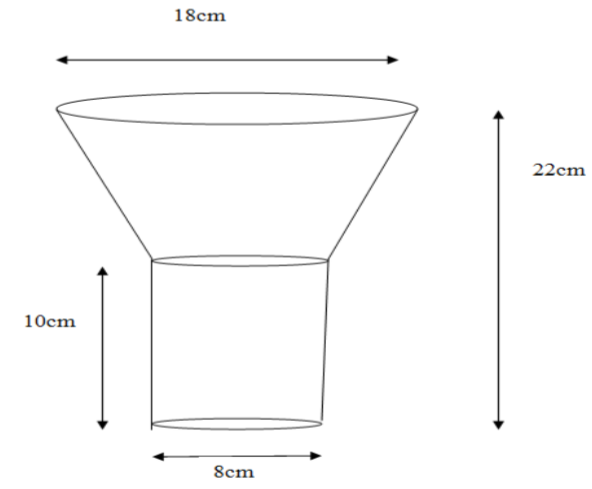
The oil funnel made of tin sheet has its upper part as frustum cone and lower part as a cylinder. We are asked to find the area required to make the tin sheet. We see that the o that is funnel is hollow inside. So we do not tin sheet for the base area and only need for the curved surface area. \[\]

It is given that the diameter of the cylinder at the lower part of the funnel is 8cm. So the radius of the lower base is $r=\dfrac{8}{2}=4cm$. The height is given $h=10$cm. So the curved surface area of the cylinder is ${{A}_{1}}=2\pi \left( 4 \right)\left( 10 \right)=80\pi \text{c}{{\text{m}}^{\text{2}}}$\[\]
We see in the upper part that a frustum cone has height which is the difference of height of the funnel and the height of the cylinder. So height of frustum cone is ${{h}_{c}}=22$cm, the diameter of the upper base 18cm, so its radius is ${{r}_{1}}=\dfrac{18}{2}=9$cm. The radius of the lower base is the same as the radius of the cylinder ${{r}_{2}}=4$cm. So the slant height is
\[\begin{align}
  & l=\sqrt{{{h}^{2}}+{{\left( {{r}_{1}}-{{r}_{2}} \right)}^{2}}} \\
 & =\sqrt{{{12}^{2}}+{{\left( 9-4 \right)}^{2}}} \\
 & =\sqrt{144+25} \\
 & =13 \\
\end{align}\]
So the curved surface area of the frustum cone is ${{A}_{2}}=\pi \left( {{r}_{1}}+{{r}_{2}} \right)l=\pi \left( 9+4 \right)13=169\pi \text{c}{{\text{m}}^{\text{2}}}$

So the total surface area of funnel is sum of curved surface area of the cylinder and cone,
\[{{A}_{1}}+{{A}_{2}}=80\pi +169\pi =249\pi =249\times 3.14=781.6\text{c}{{\text{m}}^{\text{2}}}\]

Note: The important thing we notice here is we do not add the base area because the inside of a funnel is hollow. The total surface are of a cylinder is $2\left( \pi rh+\pi {{r}^{2}} \right)$ and the total surface area of frustum cone is $\pi \left( {{r}_{1}}+{{r}_{2}} \right)l+\pi {{r}_{1}}+\pi {{r}_{2}}$.