
An unstable heavy nucleus at rest breaks into two nuclei which move away with velocities in the ratio of 8: 27. The ratio of the radii of the nuclei (assumed to be spherical) is:
A.
B.
C.
D.
Answer
493.2k+ views
1 likes
Hint: From the ratio of the velocities, we will be able to determine the ratio of their atomic masses by using the momentum conservation theorem. Next, using the formula for the radius of a nuclei, we will be able to find the ratio of their radii.
Formula Used: Momentum conservation theorem:
Where
Radius of a nuclei:
Where
Complete step by step answer:When an unstable nuclei fissions, it breaks into two nuclei which move away at a particular velocity like shown below:
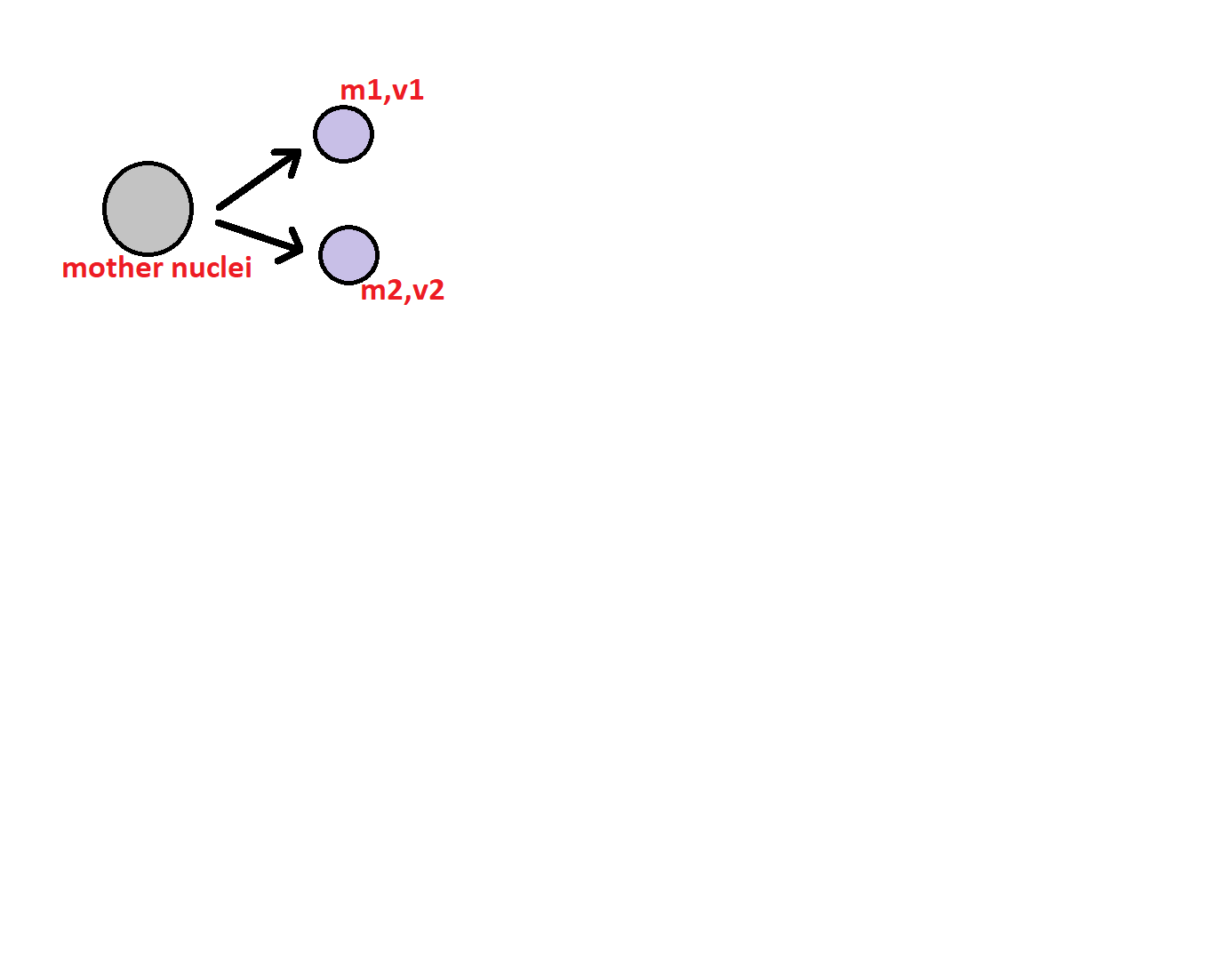
This system has conservation of momentum at all points. Therefore we can say that
Upon rearrangement we get,
Substituting the values we get,
For nuclei, mass will be represented using
Now, we know that
Taking this formula for each nuclei we get,
Dividing these two we get,
Substituting the values of
Therefore, the ratio of their radii is
In conclusion, the correct option is C.
Note:It is interesting to see the law of conservation of momentum of classical physics being applied in quantum physics. This was assumed as a case of general two bodies in motion and therefore the law helped us solve it easily.
Formula Used: Momentum conservation theorem:
Where
Radius of a nuclei:
Where
Complete step by step answer:When an unstable nuclei fissions, it breaks into two nuclei which move away at a particular velocity like shown below:

This system has conservation of momentum at all points. Therefore we can say that
Upon rearrangement we get,
Substituting the values we get,
For nuclei, mass will be represented using
Now, we know that
Taking this formula for each nuclei we get,
Dividing these two we get,
Substituting the values of
Therefore, the ratio of their radii is
In conclusion, the correct option is C.
Note:It is interesting to see the law of conservation of momentum of classical physics being applied in quantum physics. This was assumed as a case of general two bodies in motion and therefore the law helped us solve it easily.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Class 12 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Trending doubts
Draw a labelled sketch of the human eye class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Which one of the following is a true fish A Jellyfish class 12 biology CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Write the difference between solid liquid and gas class 12 chemistry CBSE




