Question

What is the angle (in circular measure) between the hour hand and minute hand of a clock when the time is half-past $4$?
A. $\dfrac{\pi }{3}$
B. $\dfrac{\pi }{4}$
C. $\dfrac{\pi }{6}$
D. None of these

Answer 1

Hint: A clock has a shape of the circle made up of ${360^ \circ }$ , as a clock has $12$ hours, each hour will draw an angle measure of $360/12$ i.e., ${30^ \circ }$ . By drawing a clocking diagram in this case minute hand will be at $6$ i.e., $30$ minutes and the hour hand is exact in between $4$ and $5$. In this way, we have to approach the problem.

Complete step-by-step answer:
The clock diagram of half past 4 i.e., $4:30$.

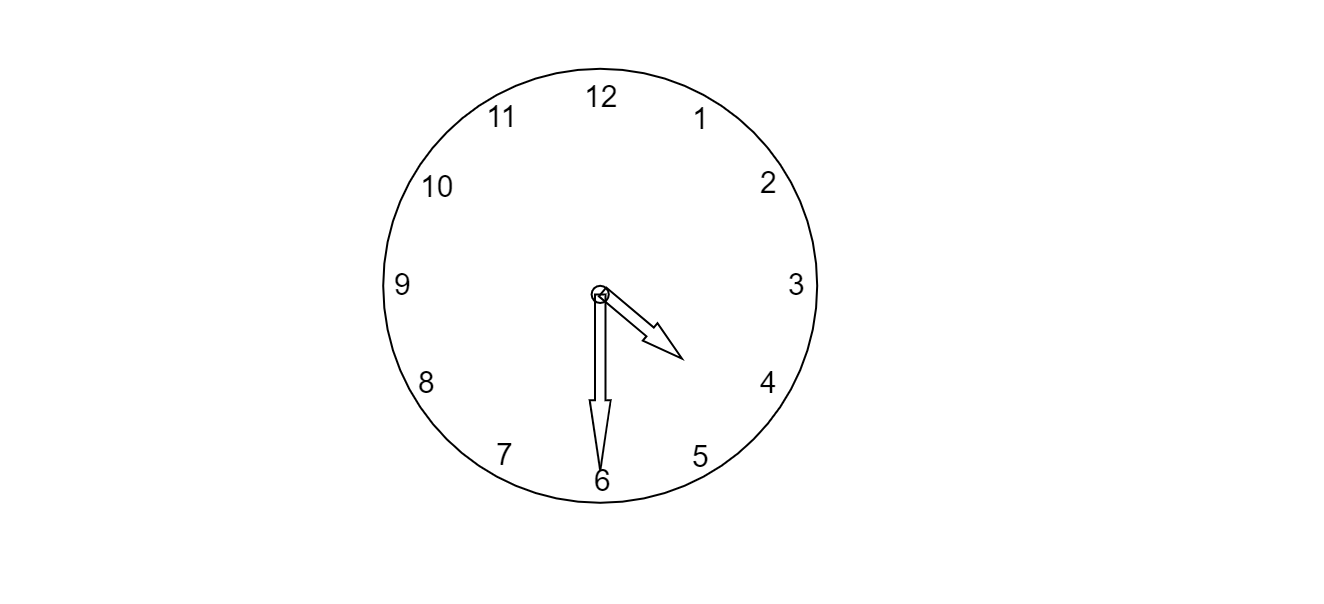
In the clock the angle between each hour division will be $\dfrac{{360}}{{12}} = {30^ \circ }$
The angle between $5$ and $6$ will be ${30^ \circ }$ as there is a gap of an hour.
At $4:30$, the hour hand will become the angle bisector between $4$ and $5$ .
As $4$ and $5$form an hour gap, the angle between them will be ${30^ \circ }$ and the hour hand bisects them so we will divide the angle of one hour by $2$ i.e., $\dfrac{{30}}{2} = {15^ \circ }$
So the total angle between the hour hand and minute hand at half-past $4$will be equal to the angle between $5$ and $6$plus the angle which divides $4$ and $5$in equal parts.
The angle between the hour hand and minute hand at half past $4$= ${30^ \circ }$ + ${15^ \circ }$ = ${45^ \circ }$.
Converting the degree angle to radian angle:
Angle in radian = angle in degree $ \times \dfrac{\pi }{{{{180}^ \circ }}}$
Angle in radian = ${45^ \circ } \times \dfrac{\pi }{{{{180}^ \circ }}}$
Angle in radian = $\dfrac{\pi }{4}$
Therefore, the angle between the hour hand and minute hand at half-past $4$is $\dfrac{\pi }{4}$ .
The correct option is option B. $\dfrac{\pi }{4}$
So, the correct answer is “Option B”.

Note:We can illustrate by representing the clock diagram and timing is $12$ o’clock and observe the minute hand and hour hand makes a straight line so we can directly say that angle is ${0^ \circ }$similarly if the question is asked about $6$o’clock then also illustrate a diagram for that then you can directly say that angle between hands is ${180^ \circ }$.