Question

Angle of deviation is the angle which the ................. ray makes with the direction of ................. ray.

(A) emergent, incident

(B) incident, emergent

(C) incident, incident

(D) emergent, emergent

Answer 1

Hint: The given problem can be seen as a ray of light passing through a prism i.e. an optical instrument and follows the rules of ray optics. For understanding these types of problems, we can study about the optical instrument prism and how it works.

Step-by-step solution:
Step 1: First of all, we can see the definition, geometry, and working of prisms and by going through its working principle we will be able to define the angle of deviation.
Prism: A prism is a portion of a transparent medium bounded by two plane faces inclined to each-other at a suitable angle. These two planes are the two refractive faces of the prism and the angle between these two faces is known as refractive angle or angle of prism.
The line where these two refracting faces meet is known as the refracting edge of prism.
Working: When a ray of light passes through a prism then it is refracted two times through the prism and hence deviates through a certain angle from its original path and this deviation from its path is known as the angle of deviation.

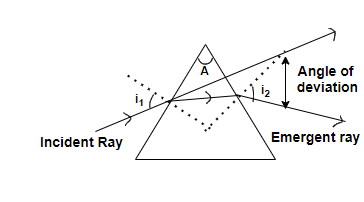
So, we can define the angle of deviation in such a way that when an incident ray passes through a prism then it gets deviated two times at both the refracting surfaces of the prism. So, the angle of deviation is the angle which the emergent ray makes with the direction of incident ray, when this ray is passed from one medium to another at the refracting surfaces of the prism then creates an angle between the direction of refracted ray and the direction of incident ray.
 Angle of deviation is the angle which the emergent ray makes with the direction of incident ray.

So, the option (A) is correct.

Note:
1) The angle of deviation can be calculated by the given formula –
$$\delta =i_1+i_2-A$$ …………..(1)
Where $$\delta =$$ the angle of deviation, $$i_1=$$ angle made by the incident ray of light at prism face, $$i_2=$$ angle made by the refracted ray at second surface going from one medium to another, and $$A=$$ angle of prism.
And, $$\delta =\left(\mu -1\right)A$$........................(2)
Where $$\mu =$$ refractive index of the material of the prism, and $$A=$$ angle of prism.
2) When refracting angle of the prism is small ($$<{10}^{\circ }$$), the deviation $$\delta$$ is calculated from equation (2) and when refracting angle of prism is large, the deviation $$\delta$$ is calculated from equation (1).