Question

Angle of dip $\delta$ and latitude $\lambda$, on earth’s surface are related as

A.$\tan { \delta =2\tan { \lambda } }$
B.$\tan { \delta =\cot { \lambda } }$
C.$\tan { \delta =\dfrac { \tan { \lambda } }{ 2 } }$
D.$\tan { \delta =\tan { \lambda } }$

Answer 1

Hint: Using the formula for magnetic field find the magnetic field at position r. Then, find the magnetic field at $\theta$. But, $ \theta =90+\lambda$ , so substitute this value in the equation for magnetic field for r as well as $\theta$. Now, take the ratio of these obtained magnetic fields and get the relation between angle of dip $\theta$ and latitude $\lambda$.
Formula used:
${ B }_{ r }=\dfrac { { \mu }_{ 0 } }{ 4\pi } \dfrac { 2M\cos { \theta } }{ { r }^{ 3 } }$
${ B }_{ \theta }=\dfrac { { \mu }_{ 0 } }{ 4\pi } \dfrac { M\sin { \theta } }{ { r }^{ 3 } }$

Complete answer:
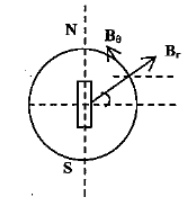
Consider the situation for dipoles at positions, r and $\theta$
The magnetic field at position r is given by,
${ B }_{ r }=\dfrac { { \mu }_{ 0 } }{ 4\pi } \dfrac { 2M\cos { \theta } }{ { r }^{ 3 } }$ …(1)
The magnetic field at $\theta$ is given by,
${ B }_{ \theta }=\dfrac { { \mu }_{ 0 } }{ 4\pi } \dfrac { M\sin { \theta } }{ { r }^{ 3 } }$ …(2)
But, $ \theta =90+\lambda$ …(3)
Thus, substituting the equation. (3) in equation. (2) we get,
${ B }_{ r }=\dfrac { { \mu }_{ 0 } }{ 4\pi } \dfrac { 2M\cos { 90+ \lambda } }{ { r }^{ 3 } }$
$\Rightarrow { B }_{ r }=\dfrac { { \mu }_{ 0 } }{ 4\pi } \dfrac { M\sin {\lambda} }{ { r }^{ 3 } }$ …(4)
Similarly. Equation. (2) becomes,
${ B }_{ \theta }=\dfrac { { \mu }_{ 0 } }{ 4\pi } \dfrac { M\sin { 90+ \lambda } }{ { r }^{ 3 } }$
${ B }_{ \theta }=\dfrac { { \mu }_{ 0 } }{ 4\pi } \dfrac { M\cos {\lambda} }{ { r }^{ 3 } }$ …(5)
Dividing equation.(4) by (5) we get,
$\dfrac { { B }_{ r } }{ { B }_{ \theta } } =-2\tan { \lambda }$
Or we can also write it as,
$\tan { \delta =\tan { \lambda } }$

Hence, the correct answer is option D i.e. $\tan { \delta =\tan { \lambda } }.$

Note:
Here, the angle of dip means the angle of magnetic dip. Magnetic dip is defined as an angle which is made between the Earth’s magnetic field lines and horizontal plane. This angle is not constant. It depends on the point that is taken into consideration. And by latitude, we mean magnetic latitude. It is different from geographic latitude. It is defined with respect to the magnetic dipoles.