Question

What is the angle of incidence of a ray if the reflected ray is at an angle of \[{90^{\text{o}}}\] to the incident ray?

Answer 1

Hint: In this question, we should learn the law of reflection. Consider the angle of incidence as \[i\] and consider the angle of reflection as \[r\]. The angle of incidence is always measured in between the incident ray and the normal ray.

Complete step by step answer
 In this question, we must consider the figure (1) to show the incident ray, reflected ray and the normal at the point of incidence that lie in the same plane.
So, the incident ray of light falls on the surface and makes the angle with the normal that is \[i\], and the angle made by reflected ray with the normal is \[r\] which is normal to the bottom of the surface. We are given that the reflected ray at an angle of incidence is \[{90^{\text{o}}}\].
When the ray of light passes through and that is incident on the surface, so that ray gets reflected in a certain direction.
 

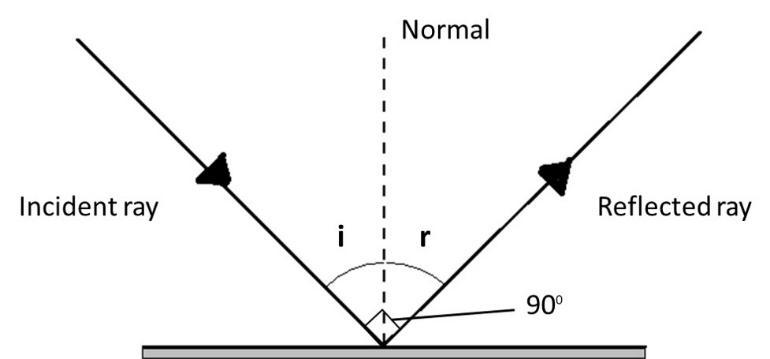
                                       Figure (1)
As we know that the incident angle is the angle made by the incident ray with the normal at the point of incidence and the reflected angle is the angle made by the reflected ray with the normal at the point of incidence.
Now we use the law of reflection, this law says that incident angle is equal to the reflected angle. So,
\[ \Rightarrow \angle i = \angle r\]
Now we write the equation as per given in the question,
\[ \Rightarrow \angle i + \angle r = {90^{\text{o}}}\]
Let us assume that the angle be \[x\] and substitute in the above equation as,
\[ \Rightarrow x + x = {90^{\text{o}}}\]
After adding the values, we get,
\[ \Rightarrow 2x = {90^{\text{o}}}\]
\[\therefore x = {45^{\text{o}}}\]
Thus, the angle of incidence is \[{45^{\text{o}}}\]


Therefore, the reflected ray is at an angle of \[{90^{\text{o}}}\] to the incident ray , then the angle of incidence is \[{45^{\text{o}}}\].

Note
As we know that the angle of incidence is equal to the angle of reflection, \[\angle i = \angle r\], and the reflected ray and incident ray and the normal at the point of incidence all these lie on the same plane.