Question

What is the angle sum of a polygon with $9$ sides?

Answer 1

Hint: To solve this question we need to know the concept of polygon and angles. A polygon with $9$ sides is called nonagon. The first step is to mark a point in the interior of the polygon. Second step is to connect the point with each vertex which form triangles. We will apply the angle sum property to each triangle and will then subtract the total angle with ${{360}^{\circ }}$.

Complete step-by-step answer:
The question asks us to find the sum of the interior angles in a nonagon which is a polygon with $9$ sides. Nonagon is a regular polygon with $9$ sides. The first step is to mark a point $O$ at the centre, and then join each vertex of the polygon with that point as shown in the figure below.

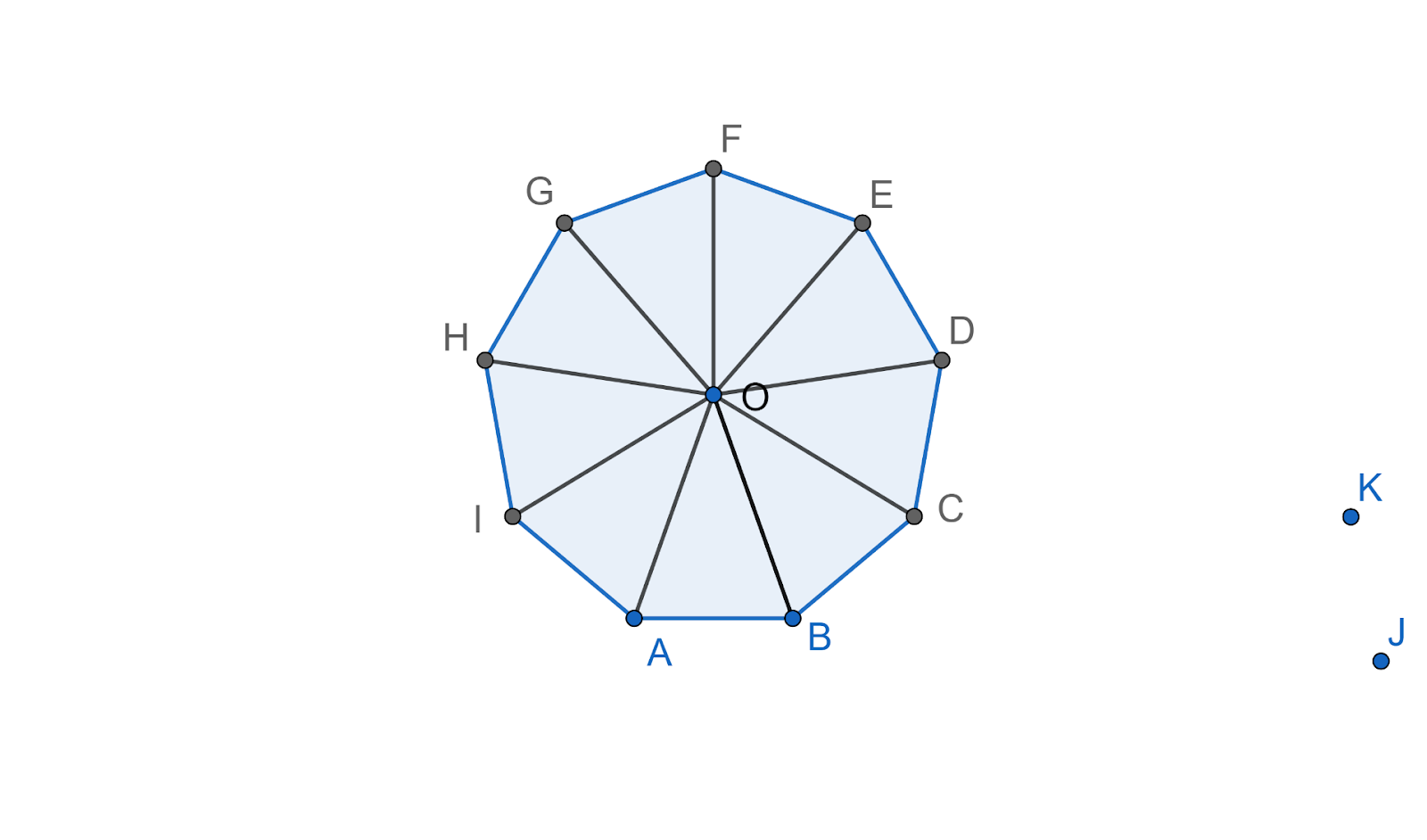
On counting the total number of triangles formed by the connecting vertices and the point $O$ we get a total of $9$ triangles.
We know that the sum of angles of a triangle is equal to ${{180}^{\circ }}$ . Since there are $9$ triangles formed in a nonagon, therefore the total angle subscribed will be $9$ times ${{180}^{\circ }}$. Mathematically it will be written as:
$= 9\times {{180}^{\circ }}$
On multiplying
$= {{1620}^{\circ }}$
Now, we know that the angle around a point is ${{360}^{\circ }}$. The polygon contains a point $O$ so the angle surrounding the point $O$ will be ${{360}^{\circ }}$. The total sum of interior angle will be:
$= {{1620}^{\circ }}-{{360}^{\circ }}$
On subtracting the angles we get:
$= {{1260}^{\circ }}$
$\therefore $ The angle sum of a polygon with $9$ sides is ${{1260}^{\circ }}$.

Note: Instead of solving the question in such a big manner we can solve it using a formula. The formula to find the sum of the interior angles of a polygon is ${{180}^{\circ }}\left( n-2 \right)$ , here $n$ is the sides of the polygon. Applying this formula to find the total angles of the polygon where value of $n$ is $9$ we get:
$= {{180}^{\circ }}\left( n-2 \right)$
$= {{180}^{\circ }}\left( 9-2 \right)$
$= {{180}^{\circ }}\left( 7 \right)$
$= {{1260}^{\circ }}$
So questions like this could be solved in this manner too.