Question

What is the angular displacement for the minute hand of a clock in 600 seconds?

Answer 1

Hint: Angular displacement of a body is the angle in radians through which a point revolves around a centre or a line that has been rotated in a specific sense about a specified axis. So we need to find the value of the angle in degrees for the minute hand of a clock in 600 seconds.

Complete answer:
We know that,
60 minutes is equal to 1 degree
So, 1 minute will be equal to ${{\dfrac{1}{60}}^{\circ }}$ (According to unitary method)
In other words, we can say,
60 seconds is equal to ${{\dfrac{1}{60}}^{\circ }}$
$\therefore $ 1 second is equal to ${{\dfrac{1}{60\times 60}}^{\circ }}$
Hence, in 600 seconds, the displacement of the minute hand is \[{{\dfrac{360\times 600}{60\times 60}}^{\circ }}\] = 60\[^{\circ }\]

Thus, the total angular displacement of the minute hand of the clock is 60 degrees.

Additional Information:
It is very important to keep in mind that 60 minutes is equal to 1 degree and 60 seconds is equal to 1 minute. Such information must be kept in mind while solving problems of this kind. There is another formula for angular displacement besides calculating the angular displacement by unitary method. The formula is as follows:
$\theta =\dfrac{l}{r}$ , where angular displacement is given by the length of the arc divided by the radius of the circle.

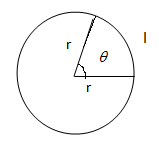
Fig: diagram showing the angular displacement, $\theta $
Angular displacement is generally calculated in radians, but it can also be expressed in degrees or revolutions per second.

Note:
 Angular displacement is usually expressed in radians. While solving problems as such, it must be remembered that angular displacement can be calculated by calculating the length of the arc and the radius of the circular motion or even from minutes and seconds by directly calculating the angle. Angular displacement is simply the displacement from initial point to final point in curvilinear motion.