Question

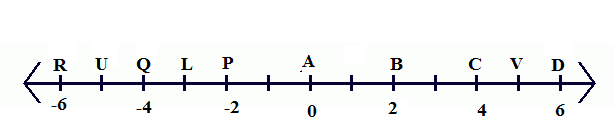
Answer the questions with the help of the figure given below. \[\]
i) State the point which are equidistant from point B.\[\]
ii) Write a pair of points equidistant from point Q.\[\]
iii) Find $d\left( U,V \right),d\left( P,C \right),d\left( V,B \right),d\left( U,L \right)$\[\]

Answer 1

Hint: We recall how points are represented on number lines. We find the number represented by alphabets U, L, and V. We move an equal number of positions or points towards left and right B and Q to get equidistant points. We count the points we cross when moving from one point to another to find the distance between them.

Complete step-by-step solution
We are given in the question a figure of a number line with only even numbers denoted. The positions of alphabets R, Q, P, A, B, C and D are represented as integral numbers$-6,-4,-2,0,2,4,6$ as points respectively. So we have
\[\begin{align}
  & R=-6,Q=-4,P=-2 \\
 & A=0,B=2,C=4,D=6 \\
\end{align}\]
We know that in the number line the increment from position to position is 1. So the position number of U will be 1 increased from the position number of R which means the position number of U is $-6+1=-5$. The position number of L is 1 increased from the position number of Q which means the position number of L is $-4+1=-3$. The position number of V is 1 increased from the position number of B which means the position number of V is $2+1=3$.So we have,
\[U=-5,L=-3,V=3\]
(i) We are asked to find the equidistant points from point B. If we move an equal number of positions towards the left and right of B we can get equidistant points. So we move 1 position towards the left of B and right of and get unnamed points. We increase 2 positions towards the left of B and right of B and get equidistant points A and C. We increase 3 positions towards the left of B and right of B and get unnamed points. We increase 4 positions towards the left of B and right of B and get equidistant points P and D. We cannot move more than 4. So the equidistant points from B are A and C, P and D. \[\]
(ii)We are asked to write a pair of points equidistant from point Q. We move 1 position towards left and right of Q and get the equidistant points as U and L. \[\]
(iii) We are asked to find $d\left( U,V \right),d\left( P,C \right),d\left( V,B \right),d\left( U,L \right)$ where $d$ represents the distance between points. The distance from one point to another point is the number of positions we have to cross while moving from one point. We move from U to V and cross 10 positions. So the distance between U and V is $d\left( U,V \right)=10$. We move from P to C and cross 6 positions. So the distance between P and C is $d\left( P,C \right)=6$. We move from V to B and cross 3 positions. So the distance between V and B is $d\left( V,B \right)=3$. We move from U to L and cross 2 positions. So the distance between U and L is $d\left( U,L \right)=2$. \[\]

Note: We note that we are moving from one point say X to another point say Y and counting the number points or positions in between them we are not including the position of X. We can alternatively calculate the distance if we know about absolute value. If the number represented by X is $n\left( X \right)$ and the number represented by Y is $n\left( Y \right)$ then their distance is absolute value of difference of $n\left( X \right),n\left( Y \right)$ that is $\left| n\left( X \right)-n\left( Y \right) \right|$.