
What are some examples of non-differentiable functions?
Answer
429.3k+ views
1 likes
Hint: A function
Complete step-by-step answer:
Some examples of non-differentiable functions are:
A function is non-differentiable when there is a cusp or a corner point in its graph. For example consider the function
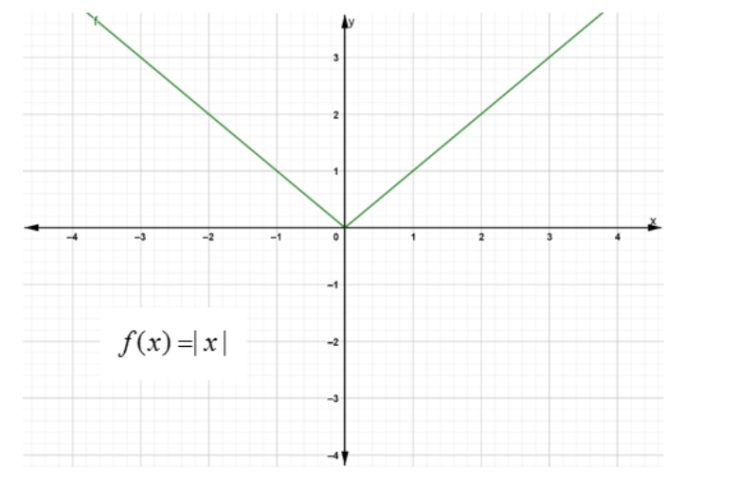
If the function is not continuous then it is not differentiable, i.e. when there is a gap or a jump in the graph of the function then it is not continuous hence not differentiable. For example consider the step function
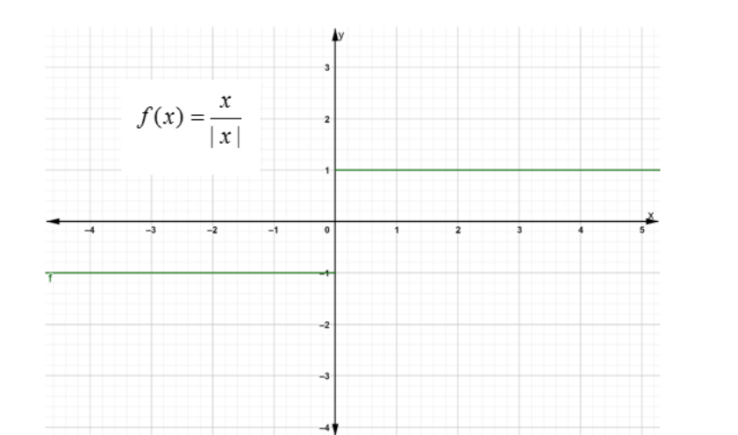
If the function can be defined but its derivative is infinite at a point then it becomes non-differentiable. This happens when there is a vertical tangent line at that point. For example, consider
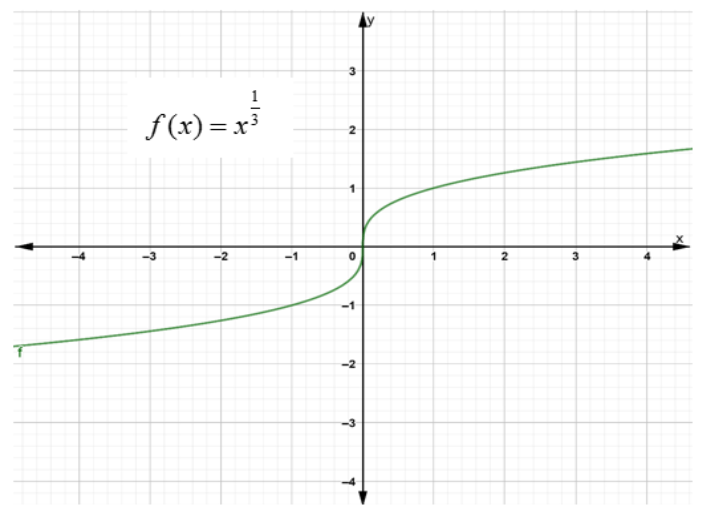
When the function is unbounded and goes to infinity at some point of its domain it becomes non-differentiable. For example consider
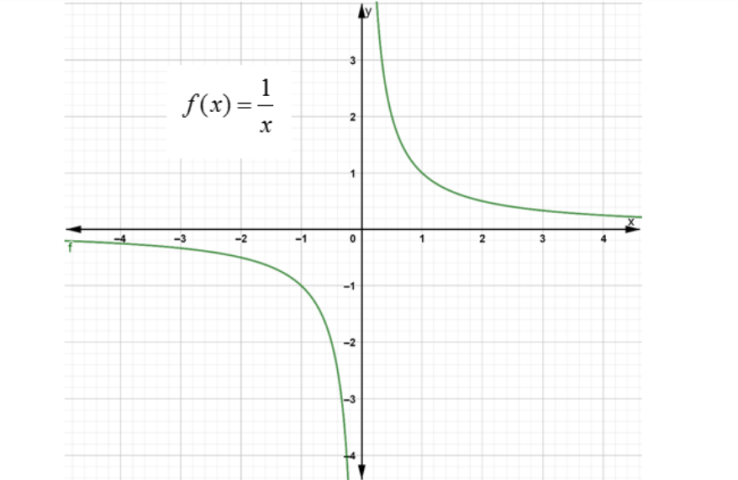
Note: If a function is differentiable then it is always continuous but the converse need not be true, i.e. there are functions which are continuous but not differentiable for example
Complete step-by-step answer:
Some examples of non-differentiable functions are:
A function is non-differentiable when there is a cusp or a corner point in its graph. For example consider the function

If the function is not continuous then it is not differentiable, i.e. when there is a gap or a jump in the graph of the function then it is not continuous hence not differentiable. For example consider the step function

If the function can be defined but its derivative is infinite at a point then it becomes non-differentiable. This happens when there is a vertical tangent line at that point. For example, consider

When the function is unbounded and goes to infinity at some point of its domain it becomes non-differentiable. For example consider

Note: If a function is differentiable then it is always continuous but the converse need not be true, i.e. there are functions which are continuous but not differentiable for example
Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 4 Maths: Engaging Questions & Answers for Success

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE




