Question

Why are tetrahedral complexes generally high spin?

Answer 1

Hint: For this, we should know about crystal field splitting in tetrahedral complexes. Same like octahedral crystal field, tetrahedral crystal field splits their orbitals into same $ {t_{2g}} $ and $ {e_g} $ sets of orbitals but the two orbitals in the $ {e_g} $ set are lower in energy now than the three orbitals in the $ {t_{2g}} $ set .

Complete answer:
A regular tetrahedron is similar to a cube. One atom at the centre of the cube and four of the eight corners of the cube contain ligands as shown in the following figure:

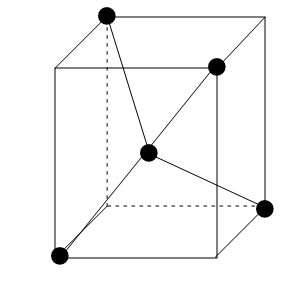
The direction $ x $ , $ y $ and $ z $ point to the centre faces of the cube. The $ {e_g} $ orbitals point along the $ x $ , $ y $ and $ z $ whereas the $ {t_{2g}} $ orbitals point between $ x $ , $ y $ and $ z $ .

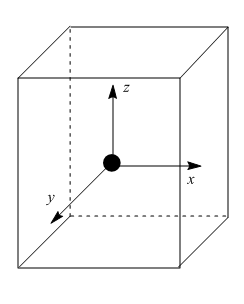
Due to which the angle between an $ {e_g} $ orbital, central metal and ligands is half of the tetrahedral angle, i.e. $ \dfrac{{{{109}^ \circ }28'}}{2} $ which is $ {54^ \circ }44' $ .On the other hand, the angle between a $ {t_{2g}} $ orbital, central metal and ligands is $ {35^ \circ }16' $ . Thus $ {t_{2g}} $ orbitals are nearer to the ligands than $ {e_g} $ orbitals. Since the approach of the ligands raises the energy of both sets of orbitals, the energy of the $ {t_{2g}} $ orbitals is raised most because they are close to the ligands as shown in figure:

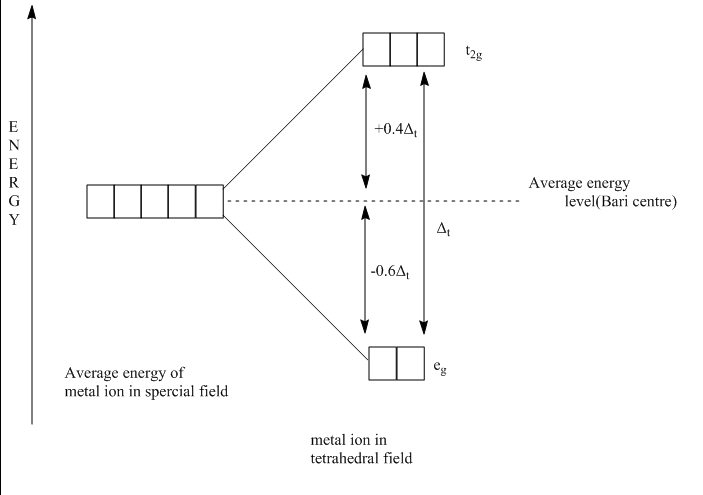
The $ {t_{2g}} $ orbitals are $ 0.4{\Delta _t} $ above the Bari centre and $ {e_g} $ orbitals are $ 0.6{\Delta _t} $ below the Bari centre. Thus, the tetrahedral crystal field splitting $ {\Delta _t} $ is $ \dfrac{2}{3} \times \dfrac{2}{3} = \dfrac{4}{9} $ of the octahedral crystal field splitting $ {\Delta _o} $ . Strong field ligands cause a bigger energy difference between $ {t_{2g}} $ and $ {e_g} $ than weak field ligands. However, the tetrahedral splitting is always much smaller than that of octahedral splitting. Thus, it is never energetically favorable to electron pairs and hence all the tetrahedral complexes have high spin.

Note:
For coordination number four, the geometry for high spin is the tetrahedral as it has $ s{p^3} $ whereas the geometry for low spin will be square planar because of $ s{p^2}d $ hybridization. Here Bari centre is the average energy level.