Question

What are the four parts of Parabola?

Answer 1

Hint: To solve this question we need to have the knowledge of parabola. Parabola is defined as the set of points in a plane that are at the same distance from a fixed line which is called Directrix and fixed point which is called focus. The question will be answered with the help of the diagram of the parabola.

Complete step-by-step solution:
The question asks us to write about the four parts of the conic section parabola. To start with, we will write about the definition of parabola. So parabola is basically a curve which is formed by a set of points which is at the same distance from a fixed line called directrix and of its point which is called focus.

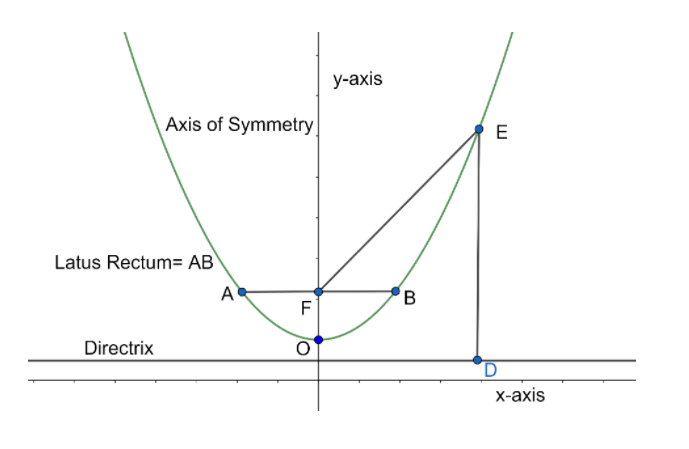
The four parts of the parabola are:
1. Y- intercept: The y-intercepts are the points or the point at which the parabola intersects the y-axis. In the above case the parabola does have a y- intercept.
2. X- intercept: The x-intercepts are the points or the point at which the parabola intersects the x-axis. In the above case the parabola does not have any x- intercept.
3. Vertex : The vertex of a parabola is the point at the intersection of the parabola and its line of symmetry. In the above diagram the vertex is denoted by $O$.
4. Axis of symmetry: The axis of symmetry of a parabola is a line about which the parabola is symmetrical.

Note: In case of the conic section parabola the point on parabola is at the same distance from focus and from the perpendicular line from the Directrix. From the diagram, the above expression is valid $FE=ED$ , where $F$ is the focus. For a conic section to be parabola the above expression is a necessity. With different curves the condition changes which results in change in the equation of the conic section.