Question

Why are there two peaks in the Compton Effect?

Answer 1

Hint :Arthur Compton gave the Compton Effect in the year 1922. During the study, Compton found out that the wavelength is not dependent on the intensity of incident radiation. It only depends upon the angle of scattering and the wavelength of the incident beam.

Complete Step By Step Answer:
Compton Effect is caused by the inelastic scattering of high-energy photons that are bound to free electrons.
In Compton Effect, an incident beam of a certain wavelength (mostly an x-ray) scatters X-rays from the electron it had made an impact upon. The scattered X-rays have their intensity peaks at two wavelengths.

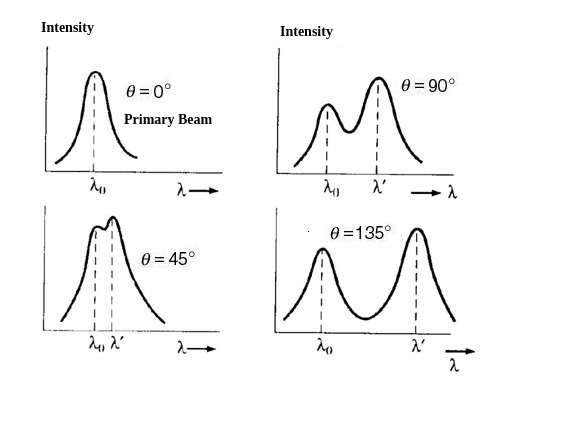
Here, $\lambda $ is the wavelength of the original photon and ${\lambda'}$ is the wavelength of the photon which has been scattered.
It is necessary to remember that some of the photons emitted from the electrons will have that same wavelength. When a photon, oscillating with a certain frequency, hits an electron, it will vibrate, or oscillate, with that same frequency. This results in emitted photons having the same value. So, in this case, the emitted photon has the same frequency and wavelength, resulting in the first peak.
In the other case, when a photon hits an electron, it transfers some of its energy, and therefore the scattered photon is less energetic, resulting in a higher wavelength.
Each of the different angles give different values of the wavelength at which the scattered photon comes out. The angle dictates the change in $\lambda $ . The two peaks are the peak values of the incident and the scattered wavelengths at different angles of scattering.

Note :
For all angles of scattering, we get two intensity peaks. One peak is located at $\lambda $ , which is the wavelength of the incident beam. The other peak is located at ${\lambda'}$ ,which is the wavelength of the scattered photon. The two peaks are separated by $\Delta \lambda $ , which directly depends on the scattering angle $\theta $ of the scattered beam. This separation $\Delta \lambda $ is called the Compton shift.