Question

What is the area under the standard normal curve to the right of z = 1.43?

Answer 1

Hint: In this problem, we have to find the area under the standard normal curve to the right of z = 1.43. We can see that this statistical problem is based on the z confidence interval for the mean. We should know that to obtain the value for the given percentage, we have to refer to the area under the Normal distribution table. We can first draw the area and split into two parts to find the z score for the given percentage.

Complete step-by-step answer:
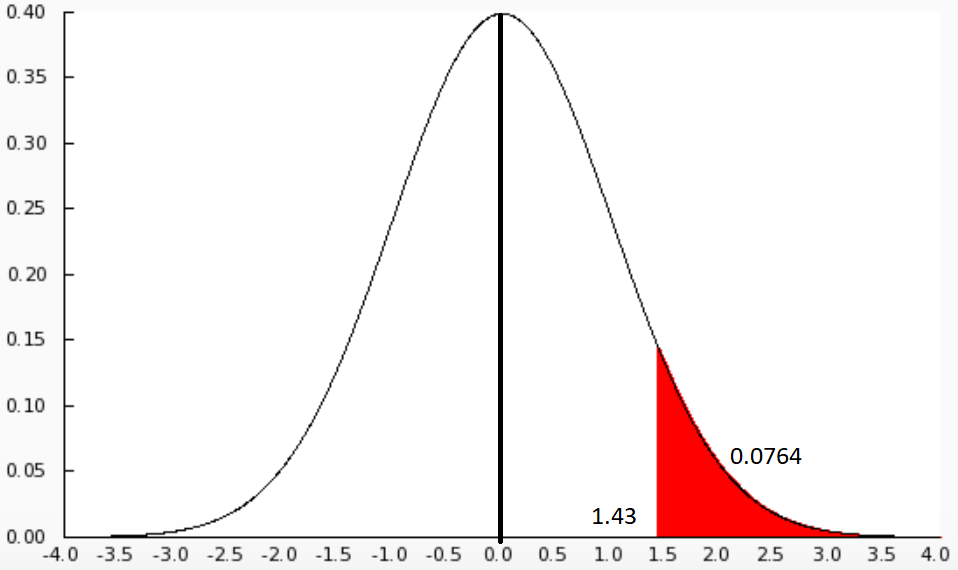
We have to find the area under the standard normal curve to the right of z = 1.43
We know that to obtain the value for the given z value, we have to refer to the area under the Normal distribution table.
We know that the area under the normal curve represents total probability, which is equal to 1 at two extreme values \[z=\infty \] and \[z=-\infty \].
We can see that the area of one half of the area is 0.5 and the value of z exactly at the middle is 0.
We have to find the area under 1.43.
We know that on one side, we have 0.5, so the remaining half will be,
\[\Rightarrow 1-0.9236=0.0764\]
Where, 0.9236 is from the standard deviation area table.
Therefore, the area under the standard normal curve to the right of z = 1.43 is 0.0764.

Note: Students make mistakes while drawing the area under the normal curve and plotting the correct points over there. We should always remember that We know that the area under the normal curve represents total probability, which is equal to 1 at two extreme values \[z=\infty \] and \[z=-\infty \]. We can see that the area of one half of the area is 0.5 and the value of z exactly at the middle is 0.