Question

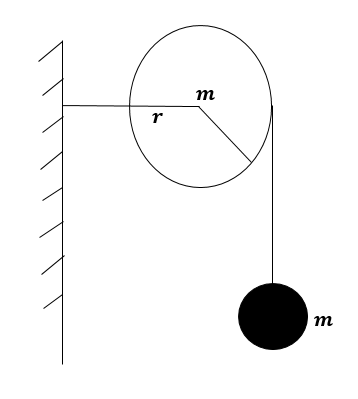
As shown in the figure, a bob of mass \[m\]is tied by a massless string whose other end portion is wound on a flywheel (disc) of radius $r$and mass $m$. When released from rest the bob starts falling vertically. When it has covered a distance of $h$, the angular speed of the wheel will be:

A. $r\sqrt {\dfrac{3}{{4gh}}} $
B. $\dfrac{1}{r}\sqrt {\dfrac{{4gh}}{3}} $
C. \[r\sqrt {\dfrac{3}{{2gh}}} \]
D. $\dfrac{1}{r}\sqrt {\dfrac{{2gh}}{3}} $

Answer 1

Hint: when the bob will be in motion. It would have kinetic energy. And the rotational motion of the flywheel will generate rotational kinetic energy. The sum of kinetic energy and rotational energy will give work done.

Formula Used: $mgh = \dfrac{1}{2}m{v^2} + \dfrac{1}{2}I{w^2}$
$I = m{k^2}$

Complete step by step answer:According to the law of conservation of energy,
$W$ (gravity)$ = \Delta K.E$(Rotational).
Where,
$W$ is work done
It is given to us that the bob is of mass $m$
Let the bob be released from rest. Then under the effect of gravity, it will fall vertically downwards.
Let it covers distance $h$ in time $t$
According to the law of conservation of energy, the potential energy that the bob had when it was at rest will be converted into kinetic energy when it starts to fall. The falling of bob will rotate the flywheel. So some of the potential energy of bob will be converted to rotation energy of the flywheel.
Rotational energy of flywheel is given as,
$K{E_r} = \dfrac{1}{2}I{w^2}$ . . . (1)
Where,
$K{E_r}$ is rotational energy
$I$ is inertia
$w$ is angular velocity of the fly wheel
We know that, for a disk of radius $r$, inertia is given by
$I = \dfrac{{m{r^2}}}{2}$
Therefore, equation (1) becomes
$ = \dfrac{1}{2}\dfrac{{m{r^2}}}{2}{w^2}$
$ \Rightarrow K{E_r} = \dfrac{{m{r^2}{w^2}}}{4}$
Since, the string is tied around the flywheel, tangential velocity, $v$ of the bob is related to its angular velocity, $w$ as
$v = wr$
Since, the potential energy is being converted into kinetic energy and rotational energy, we can say that
$PE = K{E_l} + K{E_r}$
Where,
$PE$ is potential energy
$K{E_l}$ is linear kinetic energy
$K{E_r}$ is rotational kinetic energy
$ \Rightarrow mgh = \dfrac{1}{2}m{v^2} + \dfrac{1}{2}I{w^2}$ $\left( {PE = mgh,K{E_l} = \dfrac{1}{2}m{v^2}} \right)$
$ = \dfrac{1}{2}m{w^2}{r^2} + \dfrac{{{m^2}{w^2}}}{4}$ $\left( {\because v = rw} \right)$
$ \Rightarrow mgh = \dfrac{{3m{w^2}{r^2}}}{4}$
By cancelling $m$ from both the sides, we get
$ \Rightarrow gh = \dfrac{{3{w^2}{r^2}}}{4}$
by re-arranging it, we get
${w^2} = \dfrac{{4gh}}{{3{r^2}}}$
$ \Rightarrow w = \dfrac{1}{r}\sqrt {\dfrac{{4gh}}{3}} $
Thus, the angular velocity of the flywheel will be $\dfrac{1}{r}\sqrt {\dfrac{{4gh}}{3}} $
Therefore, from the above explanation the correct option is (B) $\dfrac{1}{r}\sqrt {\dfrac{{4gh}}{3}} $.

Note:Total energy is always conserved. Work done is a scalar quantity. But it depends on the distance traveled. So if you are standing on the ground holding something in your hand, then practically you are working to hold that in your hand. But mathematically, the work done by you is zero.