Question

At some time of the day, the length of the shadow of a tower is equal to its height. Find the sun’s altitude at the times.

Answer 1

Hint: In the solution, first we have to assume a variable for the length of the shadow of a tower which is similar to the height of the tower. After that we need to apply the tangent formula to find the altitude of the sun.
$\tan \theta = \dfrac{{{\rm{perpendicular}}}}{{{\rm{base}}}}$.

Complete step by step answer:
Given, the length of the shadow of a tower = Height of the tower …… (i)
Step I: Let us assume that the length of the shadow of a tower is $x$
Therefore, the height of the tower is $x$(from equation (i)).
Let us draw a diagram according to the question.

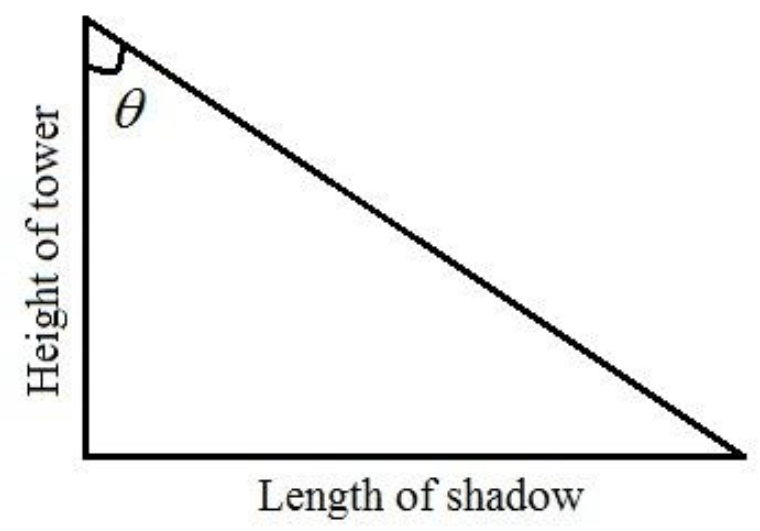
Step II:Now apply the tangent formula to calculate the altitude of the sun.
We know that
$\tan \theta = \dfrac{{{\rm{perpendicular}}}}{{{\rm{base}}}}$
Here, perpendicular is length of the shadow, that is $x$
And base is height of tower, that is $x$
Therefore, altitude of the sun is given as,
$\begin{array}{c}\tan \theta = \dfrac{{\rm{x}}}{{\rm{x}}}\\\tan \theta = 1\\\tan \theta = \tan 45^\circ \\\theta = 45^\circ \end{array}$
The value of $\theta $ is $45^\circ $.

Hence, the altitude of the sun is $45^\circ $.

Note: For a right angle triangle the trigonometric identity $tan \theta$ is the ratio of the opposite side to the adjacent side of the triangle. Here we have to determine the angle of altitude for the given data. In step I, we consider a similar variable for the length of the shadow of a tower and for the height of the tower, because according to the question, the length of the shadow of a tower = Height of the tower. Draw the diagram. Apply the tangent formula which is $\tan \theta = \dfrac{{{\rm{perpendicular}}}}{{{\rm{base}}}}$. Tangent theta is the opposite side of theta separated by the side that is perpendicular to theta. The theta's tangent is defined as y over x. Place the values in the equation. Remember that $\tan 45^\circ = 1$.