Question

At the highest point on trajectory of a projectile, its
A. potential energy is minimum
B. kinetic energy is maximum
C. total energy is maximum
D. kinetic energy is minimum.

Answer 1

Hint: In this question, first we will see the definition of projectile motion. Then we will see the expression for the horizontal and vertical component of the velocity of the particle which is projected from ground at angle $\theta $ . Then finally calculate the velocity and kinetic energy at the highest point.

Complete answer:
First of all let us see what is projectile motion?
Projectile Motion:
It is defined as the motion of the particle in a plane or 2D. Here the particle is projected from under the action of gravity of the earth. So, the acceleration acts only in a vertical direction. For the analysis of such motion, we set up two axis X-axis and Y-axis.

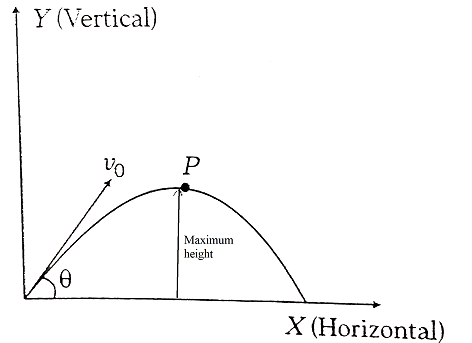
In the above projectile motion, a particle is projected at an angle$\theta $ with x- axis.
Its velocity as the function of ‘t’ can be written as:
${u_x} = {v_o}\cos \theta $ = Horizontal component of velocity.
${u_y} = {v_o}\sin \theta - gt$
Where, ‘g’ is acceleration due to gravity of earth.
The horizontal component of velocity remains constant w.r.t. time but as the particle goes upward, its vertical velocity decreases with time and at the highest point, it becomes zero.
Therefore, at the highest or at maximum height, the net velocity is u= ${v_o}\cos \theta $.

So, we can say that at the maximum height, the kinetic energy is minimum as the vertical velocity is zero.
Minimum kinetic energy = $\dfrac{1}{2}m{\left( {{v_0}\cos \theta } \right)^2}$ .

So, the correct answer is “Option D”.

Note:
You should remember the formula for horizontal and vertical velocity. The linear momentum at the highest point is $m{v_o}\cos \theta $. The path of the projectile is of parabolic nature. The acceleration throughout the projectile is ‘g’ and it acts in downward direction.