Question

Block A in the figure is released from rest when the extension in the spring is $x_0$. The maximum downward displacement of the block is:

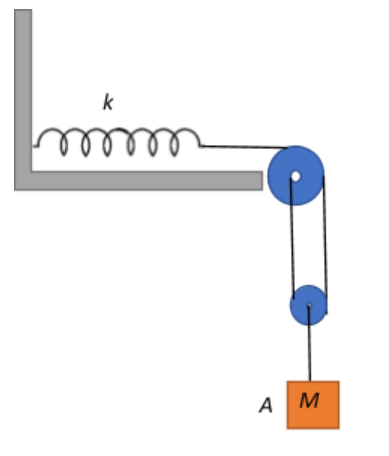
A. $\dfrac{Mg}{2k} – x_0$
B. $\dfrac{Mg}{2k} + x_0$
C. $\dfrac{2Mg}{k} – x_0$
D. $\dfrac{2Mg}{k} + x_0$

Answer 1

Hint: Begin by deducing the forces that influence our system. In other words, the forces acting on the system are gravitational force and spring force. Determine the work done by the gravitational force and the spring force. Recall that the work done by the spring force will be the difference in the potential energy possessed by the spring at initial displacement and maximum displacement. Then, use the work energy theorem to equate the work done by both the forces to the change in kinetic energy of the system. Note that the initial and final velocity of the block is zero.
To this end, solve the work-energy equation and rearrange the terms appropriately to arrive at the necessary result. Remember to account for the displacements in the lengths of the strings in the different parts of the pulley system to account for the net extension of the spring in response to these displacements.

Formula used: Work-energy theorem: $W_{net} = \Delta KE$
$W_{gravitational} = mgh$
$W_{spring} = \dfrac{1}{2}kx^2$

Complete step by step answer:
We are given that the initial extension of the spring is $x_0$. Let the maximum displacement of the string be h, i.e., block A moves down by a length of h.
From the work energy theorem which states that the net work done by the forces on an object equals the change in its kinetic energy, we have the work done by the gravitational and the spring forces to be $W_{g}$ and $W_{s}$ respectively given by:
$W_{g} + W_{s} = \Delta KE$
We are given that the block is initially released from rest. This means that its initial velocity was zero, and consequently its initial kinetic energy was zero. Also, when the block is at its maximum displacement, all its kinetic energy gets converted to potential energy and the block will be at rest, therefore, the final kinetic energy is also zero. Therefore, $\Delta KE = 0$
Therefore, $W_{g} + W_{s} = 0$.
Now, the work done by the gravitational force in holding the block at maximum displacement h is equivalent to the gravitational potential energy given as:
$W_g = PE_{gravitational} = Mgh $, where M is the mass of block A and g is the acceleration due to gravity.

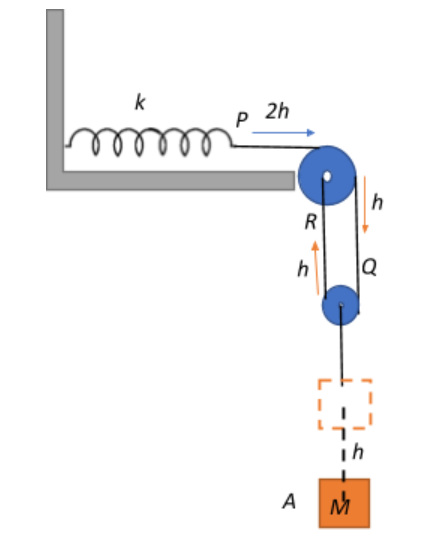
Now the work done by the spring force is equivalent to the difference in the initial and final potential energy possessed by the spring.
$W_s = U_i – U_f$
Given that the initial displacement of the spring was $x_0$, the initial potential energy stored in the spring will be:
$U_i = \dfrac{1}{2}kx_0^2$, where k is the spring constant.
The block is then displaced by $h$, which means that the string Q gets extended by h. This in turn extends the string R by h since they are all connected to the smaller pulley system, and to compensate for the extension in Q and R by h, the string P, and consequently the spring extends by h (due to Q)+h (due to R) = 2h. Therefore, the final displacement of the spring is $x_0+2h$, and the potential energy stored in the spring will be:
$U_f =\dfrac{1}{2}k(x_0+2h)^2$
Therefore $W_s = U_i -U_f = \dfrac{1}{2}kx_0^2 -\dfrac{1}{2}k(x_0+2h)^2 $
$\Rightarrow W_s = \dfrac{k}{2}[x_0 - (x_0+2h)^2]$
The above equation is in the form of $a^2 -b^2$ which we can rewrite as $(a+b)(a-b)$:
$W_s = \dfrac{k}{2}(x_0+x_0+2h)(x_0-x_0-2h) = \dfrac{k}{2}(2x_0+2h)(-2h)$
$\Rightarrow W_s = k(x_0+h)(-2h)$
Now, getting back to the work energy theorem expression and substituting $W_g$ and $W_s$, we get:
$ Mgh + k(x_0+h)(-2h)=0$
$\Rightarrow k(x_0+h)(2h) = Mgh \Rightarrow 2k(x_0+h) = Mg \Rightarrow x_0+h = \dfrac{Mg}{2k}$
$\Rightarrow h = \dfrac{Mg}{2k}-x_0$

So, the correct answer is “Option A”.

Note: Since the problem posed a multi-pulley system, calculating the net displacement of the spring accurately in response to the maximum displacement of the block becomes crucial. This is why we had to consider the extensions of the strings Q and R and their cumulative effect on the extension of P in addition to the initial displacement of $x_0$ in order to arrive at the appropriate result. Thus, whenever a pulley system is given, always try to determine the path of the strings connecting the pulleys and the loads and their responsive motion to displacement of the load.