Question

What is the Brewster angle for air to glass transition? (Refractive index of glass = 1.5)

Answer 1

Hint: Brewster angle is also called the polarizing angle. It is defined as the angle of incidence for which a beam of unpolarised light falling on a transparent surface is reflected as a beam of completely plane polarized . The refracted ray and the reflected ray makes an angle 90 with each other. Hence using Snell’s law we can obtain the Brewster angle in terms of refractive index and glass and determine the angle of polarization.

Complete answer:

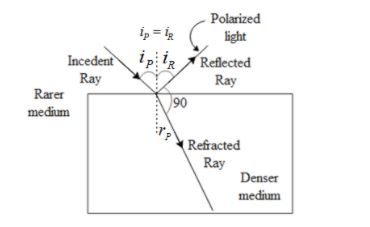
In the above figure the reflected ray makes an angle 90 degrees with the refracted ray. The Denser medium is the glass and the rarer medium surrounding it is air. Let us say the reflected ray makes an angle $i_R$ with respect to the normal of the surface of glass and the refracted ray makes an angle $r_P$with the normal of incidence. Hence we can say that,
$i_R+r_P+90=180\text{ sum of the angle along a line is 180}$. Further we can write this as $i_R+r_P=90$. Now since angle of incidence i.e. $i_P$is equal to angle of reflection, let us replace the angle of reflection by the angle of incidence. After substituting we get,
$\begin{array}{rl}& i_P+r_P=90\\ & i_P=90-r_P...(1)\end{array}$
From Snell’s law, the refractive index of the glass is given by,
$\eta ={\displaystyle \frac{\mathrm{Sin}{i}_P}{\mathrm{Sin}{r}_p}}$ , where i is the angle of incidence and r is the angle of refraction. Substituting equation 1 in the Snell’s law we get,
$\begin{array}{rl}& \eta ={\displaystyle \frac{\mathrm{Sin}{i}_P}{\mathrm{Sin}{r}_p}}\\ & \eta ={\displaystyle \frac{\mathrm{Sin}{i}_P}{\mathrm{Sin}(90-i_P)}}\text{, Since Sin(90- }\theta \text{ )=Cos }\theta \text{ ,}\\ & \eta ={\displaystyle \frac{\mathrm{Sin}{i}_P}{\mathrm{Cos}{i}_P}}=\tan i_P\\ & \mathrm{Tan}{i}_P=\eta ...(2)\end{array}$
The refractive index of glass is given as 1.5. After substituting in equation 2 we get,
$\begin{array}{rl}& \mathrm{Tan}{i}_P=\eta \\ & \mathrm{Tan}{i}_P=1.5\\ & i_P={\tan }^{-1}1.5={56.3}^{\circ }\end{array}$
Hence the Brewster angle for glass is 56.3 degrees.

Note: The angle of incidence for which the reflected light will get polarized depends on the medium on which the light is incident on. To be more precise, it also depends on both the mediums, the rarer as well as the denser. The effect of a polarized light is that the intensity of the light decreases.