Question

Calculate packing efficiency in simple cubic lattice.

Answer 1

Hint: Packing efficiency is a fraction of the unit cell actually occupied by spheres. It is the percentage of space covered by atoms to the actual space of the unit cell. Simple cubic is a type of primitive unit cell.
Formula used = $\left( {\dfrac{{volume{\text{ }}of{\text{ }}spheres}}{{volume{\text{ }}of{\text{ }}cube}}} \right) \times 100$

Complete step by step answer:
We know packing efficiency is the measure of how closely spheres are bound in a crystal lattice. Simple cubic lattice is a type of unit cell in which atoms are present only at corners (also called primitive cells).

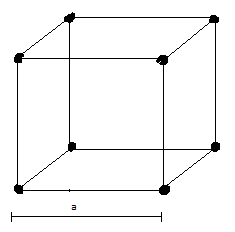
Above picture shows a simple cubic lattice with edge length $a$. Dark points refer to the centre of atoms.
Each atom in the corner is shared by eight unit cells. This means part of one atom present in one sphere is $\dfrac{1}{8}$ as it is shared by eight unit cells. There are eight corners of cube, therefore
Number of atoms$ = \dfrac{1}{8} \times 8 = 1$
There is one atom per unit cell in a simple cubic lattice.
Formula to calculate packing efficiency is
Packing efficiency$ = \left( {\dfrac{{volume{\text{ }}of{\text{ }}spheres}}{{volume{\text{ }}of{\text{ }}cube}}} \right) \times 100$
In the lattice atom is represented as a sphere so volume of sphere in formula is equivalent to volume of atom.
On one edge there will be two atoms and both atoms will touch each other so if we take the radius of the sphere to be $r$ then edge length $a$ will be equal to $2r$ (as there are two spheres with their centre at corner of cube).
$a = 2r$
volume of sphere$ = \dfrac{4}{3}\Pi {r^3}$
volume of cube$ = sid{e^3} = {a^3}$
As written above $a = 2r$
So, volume of cube$ = {\left( {2r} \right)^3} = 8{r^3}$
Packing efficiency$ = \dfrac{{\dfrac{4}{3}\Pi {r^3}}}{{8{r^3}}} \times 100$
$ = \dfrac{{100}}{6}\Pi $
$ = 52.35\% $ Which is approximately equal to $52.4\% $

Note:
In simple cubic unit cell atoms are present only at corners. It is a primitive unit cell. In other unit cells atoms are present at corners as well as at other positions. In body centered cubic lattice atoms are present at corners as well as at the centre of the cube, in face centered cubic system atoms are present at corners as well as at the center of each face of the cube.