Question

Calculate the difference of anticlockwise and clockwise moments

A. 0gf cm
B. 10gf cm
C. 1000gf cm
D. 100gf cm

Answer 1

Hint: Here the both the forces will create moments or torques on the rod. The 150gf force will create torque in anticlockwise direction and the 250gf force will create torque in clockwise direction. Find the values of the magnitudes of the moments created by the two forces (as given) about the point O. Then take the difference between the two moments. The magnitude of moment is given as .
Formula used:
$\tau =Fr\sin \theta $

Complete answer:
Let us first understand what a moment is. A moment is a torque. When the applied force at a point on the body produces a rotational motion of the body, we say that a torque or a moment has been created on the body.
Torque is always about an axis or a point of rotation. It is a vector quantity.

The value of the torque at a point about an axis or a point is given as $\overrightarrow{\tau }=\overrightarrow{r}\times \overrightarrow{F}$.
Here, $\overrightarrow{r}$ is the position vector of the point with respect to the axis or the point. $\overrightarrow{F}$ is the force applied at this point.
The magnitude of the torque is given as $\tau =Fr\sin \theta $, where $\theta $ is the angle between $\overrightarrow{F}$ and $\overrightarrow{r}$.

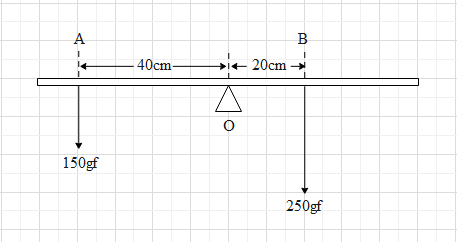
In the given case, there is a rod, which is hinged at point O. Therefore, the point O acts as the fixed axis of rotation. Meaning the rod will rotate about this point.
Let us consider the point O as the origin.
In the question, the difference of the magnitudes of the torques is asked
Hence, let us calculate the magnitude of the moments created by each of the forces.
Let us consider the force of 150gf. Let this force be ${{F}_{1}}$. It is acting at point A, which is at a distance of 40cm from point O. Let the distance of point A be ${{r}_{1}}$. Since ${{F}_{1}}$ and ${{r}_{1}}$ are perpendicular, the angle between ${{F}_{1}}$ and ${{r}_{1}}$ is ${{90}^{0}}$.

Therefore, the magnitude of the moment due to force ${{F}_{1}}$ is ${{\tau }_{1}}={{F}_{1}}{{r}_{1}}\sin 90={{F}_{1}}{{r}_{1}}=150\times 40=6000gfcm$.

Let us now consider the force of 250gf. Let this force be ${{F}_{2}}$. It is acting at point B, which is at a distance of 20cm from point O. Let the distance of point B be ${{r}_{2}}$. Since ${{F}_{2}}$ and ${{r}_{2}}$ are perpendicular, the angle between ${{F}_{2}}$ and ${{r}_{2}}$ is ${{90}^{0}}$.
Therefore, the magnitude of the moment due to force ${{F}_{2}}$ is ${{\tau }_{2}}={{F}_{2}}{{r}_{2}}\sin 90={{F}_{2}}{{r}_{2}}=250\times 20=5000gfcm$.
Therefore, the difference in the moment about point O is ${{\tau }_{1}}-{{\tau }_{2}}=6000-5000=1000gfcm$.

So, the correct answer is “Option C”.

Note:
Note that gf is a unit of force.
Also, note that we found the difference of the magnitudes of moments and not the difference between the vectors.
If the consider the directions of the moments, The torque generated by ${{F}_{1}}$ is +6000$\widehat{k}$ and the torque generated by ${{F}_{2}}$ is -5000$\widehat{k}$.
Therefore, when we calculate the difference of this two moments it will be equal to $6000\widehat{k}-(-5000\widehat{k})=6000\widehat{k}+5000\widehat{k}=11000\widehat{k}$.