Question

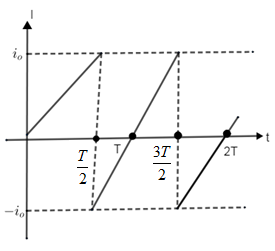
Calculate the mean and R.M.S values for a current varying as shown in graph over a period of t = 0 to t = T. the mathematical expression may be given as $i=\left( \dfrac{2{{i}_{0}}}{T} \right)t$.

Answer 1

Hint: We have been provided with a graph of current and time. Value of current is $i=\left( \dfrac{2{{i}_{0}}}{T} \right)t$ and we need to find the mean and R.M.S value of current. If the area covered by the wave is in full cycle then the average value tends to zero. Now to find R.M.S value, use expression of root mean square which is given as, $\sqrt{<{{I}^{2}}>}\text{ or }\sqrt{< i{{>}^{2}}}$
Put the value of $< i{{>}^{2}}$ and get the value of R.M.S.

Formula used: ${{I}_{rms}}=\sqrt{\text{mean of squares of instantaneous value}}$

Complete step by step answer:
We have been provided with a graph for current over a period of t = 0 to t = T. The mathematical expression of current is given by,
$i=\left( \dfrac{2{{i}_{0}}}{T} \right)t$

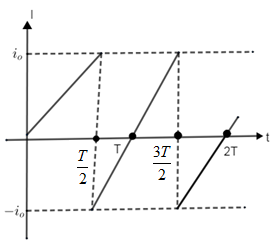
Now we need to calculate the mean and R.M.S value of a varying current. The average of all the instantaneous values of current over one complete cycle is called the mean value of current. As you can see in the figure, the graph has a triangular waveform; the positive half cycle is exactly equal to the negative half cycle. Therefore mean value over a complete cycle will be zero.
Hence the mean value of current is zero. R.M.S value of current is nothing but square root of mean value of square of current.
$ < i{{>}^{2}}=\dfrac{\int\limits_{0}^{T}{{{i}^{2}}}dt}{T}$
Put value of current
$i=\left( \dfrac{2{{i}_{0}}}{T} \right)t$
$\begin{align}
  & < i{{>}^{2}}=\dfrac{\int\limits_{0}^{T}{{{\left[ \left( \dfrac{2{{i}_{0}}}{T} \right)t \right]}^{2}}dt}}{T} \\
 & < i{{>}^{2}}=\dfrac{4{{i}_{o}}^{2}}{{{T}^{3}}}\int\limits_{0}^{T}{{{t}^{2}}}dt \\
 & < i{{>}^{2}}=\dfrac{4{{i}_{0}}^{2}}{{{T}^{3}}}\dfrac{\left( {{t}^{3}} \right)_{0}^{T}}{3} \\
 & < i{{>}^{2}}=\dfrac{4{{i}_{0}}^{2}}{{{T}^{3}}}\dfrac{\left( {{T}^{3}}-0 \right)}{3} \\
 & < i{{>}^{2}}=\dfrac{4}{3}{{i}_{0}}^{2} \\
\end{align}$
Hence, the R.M.S value of current is given by
$\begin{align}
  & {{i}_{rms}}=\sqrt{ < i{{>}^{2}}}=\sqrt{\dfrac{4}{3}{{i}_{0}}^{2}} \\
 & {{i}_{rms}}=\dfrac{2}{\sqrt{3}}{{i}_{0}} \\
\end{align}$
The R.M.S value of current is $\dfrac{2}{\sqrt{3}}{{i}_{0}}$

Additional Information: R.M.S stands for root mean square. When steady current flows through a resistor for a given period of time then as a result the same quantity of heat is produced by the alternating current, when current flows through the same resistor for the same period of time it is called root mean square value or effective value of alternating current. And it is given as,
${{I}_{rms}}=\sqrt{mean\text{ of squares of instantaneous value}}$
R.M.S value is the actual value of an alternating quantity (AC) which tells us an energy transfer capability of an AC source.

Note: The waveform given in the graph has a symmetric nature. Area of current and time are equal but with opposite signs in the first half cycle of the triangular wave and in the second half cycle of the triangular wave. Mean value is nothing but the average value of current. The work is done by both (positive and negative cycle). Hence the average value or mean value of current is determined without considering the signs.