
Calculate the moment of inertia of a thin ring of mass
Answer
511.8k+ views
Hint: We can solve this problem by considering an infinitesimal part of the wire of infinitesimal mass and finding out the moment of inertia about the axis of this infinitesimal mass. We will then find out a relation of the infinitesimal mass with some other variable of the ring such as its radius to integrate and find out the moment of inertia of the whole ring.
Formula used:
The moment of inertia
Complete step by step answer:
We will find out the moment of inertia of the thin uniform ring by first finding out the moment of inertia of an infinitesimal part of the ring of infinitesimal mass about the required axis. Then, we will proceed to find out a relation between this mass and some other variable of the ring such as its radius or circumference to integrate the moment of inertia with respect to this variable and find out the moment of inertia of the whole ring.
So let us proceed in this way.
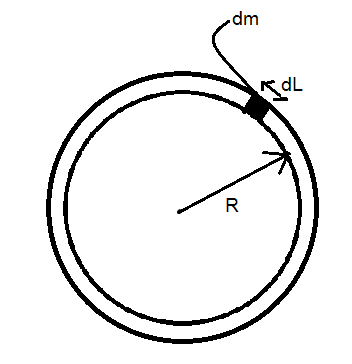
We have a thin ring of mass
Therefore the total length
Since, the ring is uniform, it must have a constant mass per unit length
We take an infinitesimal strip of length
The moment of inertia
Therefore, the moment of inertia of the infinitesimal mass about the axis passing through the center of the ring and perpendicular to its plane will be, using (3),
Now, integrating both sides with the respective variable to cover the whole ring, we get,
Hence, the required moment of inertia of a ring about an axis passing through its center and perpendicular to its pane is
Note: This is the most general and best approach to finding out the moment of inertia of different uniform bodies. However, students should have some important moment of inertia of some bodies like a sphere, disc, etc. memorized as without these most rotational mechanics problems cannot be solved. However, this approach is only applicable for uniform bodies. For non-uniform bodies it is not so easy to integrate the moment of inertia for the whole body using just one relation.
Many moments of inertia can be found out using the parallel and perpendicular axis theorems and students should understand those two very well as they are very helpful especially in competitive exams.
Formula used:
The moment of inertia
Complete step by step answer:
We will find out the moment of inertia of the thin uniform ring by first finding out the moment of inertia of an infinitesimal part of the ring of infinitesimal mass about the required axis. Then, we will proceed to find out a relation between this mass and some other variable of the ring such as its radius or circumference to integrate the moment of inertia with respect to this variable and find out the moment of inertia of the whole ring.
So let us proceed in this way.

We have a thin ring of mass
Therefore the total length
Since, the ring is uniform, it must have a constant mass per unit length
We take an infinitesimal strip of length
The moment of inertia
Therefore, the moment of inertia of the infinitesimal mass about the axis passing through the center of the ring and perpendicular to its plane will be, using (3),
Now, integrating both sides with the respective variable to cover the whole ring, we get,
Hence, the required moment of inertia of a ring about an axis passing through its center and perpendicular to its pane is
Note: This is the most general and best approach to finding out the moment of inertia of different uniform bodies. However, students should have some important moment of inertia of some bodies like a sphere, disc, etc. memorized as without these most rotational mechanics problems cannot be solved. However, this approach is only applicable for uniform bodies. For non-uniform bodies it is not so easy to integrate the moment of inertia for the whole body using just one relation.
Many moments of inertia can be found out using the parallel and perpendicular axis theorems and students should understand those two very well as they are very helpful especially in competitive exams.
Recently Updated Pages
Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Write the following in Roman numerals 25819 class 7 maths CBSE

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Write the differences between monocot plants and dicot class 11 biology CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light




