Question

How do you calculate the surface area of the lateral faces of a regular hexagonal pyramid that has a slant height of 35 cm and a base side length of 4 cm? \[\]

Answer 1

Hint: We recall the shape of a regular hexagonal pyramid which has lateral faces in congruent triangular shape. We find the area of one triangular base and multiply 6 to get the answer. We find the area of one triangle as $\dfrac{1}{2}\times \text{base}\times \text{height}=\dfrac{1}{2}\times a\times l$ where $a$ is the base side length and $l$ is the slant height. \[\]

Complete step by step answer:
We know that a Pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex. Each base edge and apex form a triangle, called a lateral face. A right pyramid has its apex directly above the centroid of its base. A pyramid that has a regular polygon base is called a regular pyramid. A regular hexagonal pyramid has its base as a regular hexagon. We draw the rough figure of it below with O as the apex and ABCDEF as the base of a regular hexagonal base. \[\]
 

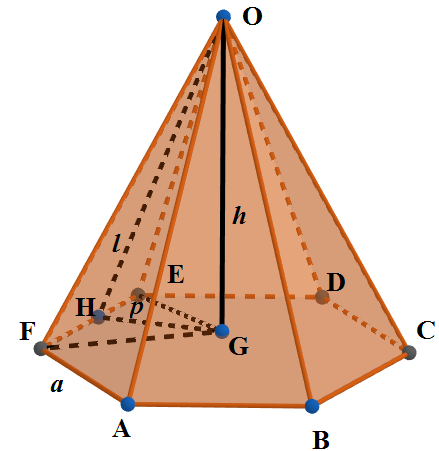
The altitude dropped from apex on the hexagon is called height of the pyramid $h=OG$ and the base side length here is $a=AB=BC=CD=DE=EF=FA$. Here $l$ is the slant height dropped from apex on one of the sides (Here OH). \[\]
 The surfaces excluding the base are called lateral surfaces and in a regular pyramid they are congruent. We have 6 lateral faces in a regular hexagonal pyramid which are in triangular shape. Since they are congruent they will be of equal area. So the surface area of the lateral faces will be 6 times the area of one triangular face. \[\]
Let us observe the triangle OEH. We know that the area of one triangle is $\dfrac{1}{2}\times \text{base}\times \text{height}$. Here base is $EF=a$ and height of triangle is slant height $l=OH$. So area of triangle OEH is
\[A=\dfrac{1}{2}\times a\times l\]
 The regular hexagonal pyramid has a slant height of 35 cm and a base side length of 4 cm. So we have $l=35$ cm, $a=4$cm. So area of one triangle is
\[A=\dfrac{1}{2}\times 4\times 35\]
We multiply 6 and find the surface area of all the lateral faces (LSA) as
\[\text{L}\text{.S}\text{.A}=6A=6\times \dfrac{1}{2}\times 4\times 35=3\times 4\times 35=420\text{ c}{{\text{m}}^{2}}\]

Note: We note that the altitude from the centre of the hexagon on a side (here$GH=p$) is called apothem. We can find the total surface area of the hexagonal pyramid as $3pa+3la$ where $3pa$ is the base area and $3la$ is the sum of lateral surface area. We can find the volume of the hexagonal pyramid as $V=p\times a\times h$.