Question

Choose the correct option provided below for the following question.
The diagonal of a rectangle is thrice its smaller side. The ratio of the sides are:
A. \[2\sqrt 2 :1\]
B. \[3:2\]
C. \[\sqrt 3 :1\]
D. $\sqrt 2 :1$

Answer 1

Hint: First, we take the sides of the rectangle as variables. With the given condition, we find the relationship between the diagonal of the rectangle and the smallest side of the rectangle and write it in terms of the taken variable. We then find the individual terms, comparing it to find the ratio between the diagonal and smallest side of the rectangle.

Complete step-by-step solution:
According to the property of rectangle, the diagonal of a rectangle is equal to the hypotenuse of the two triangles it divides.
\[ \Rightarrow \] We apply Pythagoras theorem to the formed triangles.
Draw a diagram as shown below.

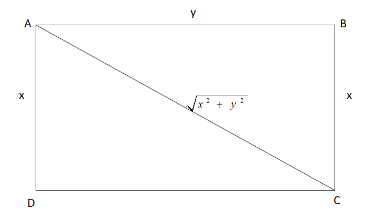
Here, let us take the smaller side, \[AD = BC = x\]
And the larger side \[AB = DC = y\]
Given the diagonal is thrice as the smallest side.
\[ \Rightarrow \] Diagonal = \[3x\]
According to the Pythagoras theorem,
\[A{C^2} = A{B^2} + B{C^2}\]
Applying square-root on both the sides:
\[AC = \sqrt {A{B^2} + B{C^2}} \]
Substituting the given values in the above equation:
\[3x = \sqrt {{x^2} + {y^2}} \]
Squaring on both sides:
\[{(3x)^2} = {(\sqrt {{x^2} + {y^2}} )^2}\]
Simplifying the terms:
\[9{x^2} = {x^2} + {y^2}\]
Rearranging the terms, we get:
\[8{x^2} = {y^2}\]
Now writing \[y\] in terms of \[x\], we get:
\[y = \sqrt {8{x^2}} \]
Taking the square root of the value, we get:
\[y = 2\sqrt 2 x\]
Now we have the values of \[x\] and \[y\].
Given the smallest side is \[AD = BC = x\]
Largest side is \[AB = DC = y\]
Diagonal is \[AC = 3x\]
The ratio between the smallest side and the largest side \[ = AD:AB\]
\[AD:AB = x:y\]
Substituting the acquired values:
\[AD:AB = x:2\sqrt 2 x\]
Cancelling out the common terms:
\[AD:AB = 1:2\sqrt 2 \]
Therefore, the ratio= \[AD:AB = 1:2\sqrt 2 \]
The ratio of the largest side to smallest side is \[AB:AD = 2\sqrt 2 :1\]

$\therefore $ The correct option is A.

Note: We can observe that a ratio may be considered as an ordered pair of numbers, a fraction with the first number in line numerator and the second in the denominator, or as the value denoted by this fraction. Ratios of counts given by natural numbers, are rational numbers, and may sometimes be natural numbers. When two quantities are measured with the same unit, as is often the case with different units is called a rate.
The ratio is the same either taking the smallest side to the largest side or the largest side to the smallest side. The values just reverse. You have to consider the properties of the rectangle as well as the triangle in this problem