Question

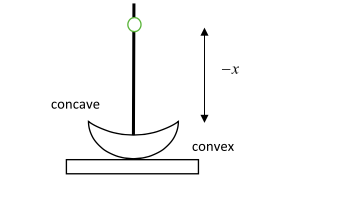
Consider a concavo-convex lens of glass of refractive index ${\mu _g} = 1.5$. The radius of curvature of the convex surface is 20 cm and that of the concave surface is 60 cm. Now, the convex surface is silvered and placed on a horizontal surface as shown in the figure below. If the concave part of the lens is filled with water of refractive index ${\mu _w} = 4\sqrt 3 $, find the distance through which the pin must be moved so that the image of the pin coincides with it:

A) $\Delta x = 1.15{\text{cm, up}}$
B) $\Delta x = 3.15{\text{cm, down}}$
C) $\Delta x = 0.05{\text{cm, up}}$
D) $\Delta x = 1.15{\text{cm, down}}$

Answer 1

Hint:The processes involved in this arrangement include refraction of the incident ray at the water- glass interface followed by the reflection of the refracted ray by the silvered convex surface and finally refraction at the glass-water interface. The light rays incident on the convex surface of the lens are reflected since the convex surface is coated with silver i.e., the convex surface acts as a mirror.

Complete step by step answer.
Step 1: List the data provided in the question.
Given, the radius of curvature of the convex surface is 20 cm and that of the concave surface is 60 cm.
Also given, the refractive index of glass is ${\mu _g} = 1.5$ and that of water is ${\mu _w} = 4\sqrt 3 $ .
A total of three processes take place in this arrangement – refraction, reflection and again refraction.
Initially, we consider the case where water is not present on the concave surface of the lens. Then the light from the object gets refracted at the air-glass interface. The refracted ray then gets reflected by the convex surface which is coated by silver (acts as a concave mirror). The reflected ray then gets refracted now at the glass-air interface and an image is formed. The position of the pin is placed so that its image coincides with it.
When the concave surface is filled with water the position of the image formed shifts and it no longer coincides with the position of the pin. So our aim is to find the distance through which the pin has to be moved to obtain its coinciding image when water is filled in the concave surface of the lens.
Step 2: Find the position of the image formed by the refraction at the air-glass interface.
Let $u = - x$ be the position of the pin (object) and ${v_1}$ be the position of the image formed by refraction at the air-glass interface. The radius of curvature of the concave surface is $R = - 60{\text{cm}}$(by sign convention).
Then for refraction, we use the expression $\dfrac{{{\mu _g}}}{{{v_1}}} - \dfrac{{{\mu _a}}}{u} = \dfrac{{{\mu _g} - {\mu _a}}}{R}$ ----- (1)
Substituting for $u = - x{\text{, }}{v_1}{\text{, }}{\mu _g}{\text{ = 1}}{\text{.5, }}{\mu _a} = 1$ and $R = - 60$ in equation (1)
we get, $\dfrac{{1.5}}{{{v_1}}} - \dfrac{1}{{ - x}} = \dfrac{{1.5 - 1}}{{ - 60}}$ .
Simplifying the above equation gives us $\dfrac{{1.5}}{{{v_1}}} - \dfrac{1}{{ - x}} = \dfrac{1}{{ - 120}}$
or, $120\left( {1.5x + {v_1}} \right) = - {v_1}x$ . This equation gets reduced to $180x + 120{v_1} = - {v_1}x$ .
Simplifying the above equation we get, ${v_1} = \dfrac{{ - 180x}}{{\left( {x + 120} \right)}}$ ------ (2)
Equation (2) represents the position of the image formed by refraction.
This image formed at ${v_1}$ then acts as the object for reflection at the convex surface.
Step 3: Find the position of the image formed by reflection from the silver-coated convex surface.
The silver-coated convex surface acts as a concave mirror and its focal length $f = \dfrac{R}{2}$.
Now for reflection, the mirror equation is given by, $\dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{f}$ , or $\dfrac{1}{v} = \dfrac{1}{f} - \dfrac{1}{u}$ ----- (3).
Let the position of the image formed by reflection be ${v_2}$ then we have the position of the object as $u = \dfrac{{ - 180x}}{{\left( {x + 120} \right)}}$ and focal length will be $f = \dfrac{{ - 20}}{2} = - 10{\text{cm}}$ (by sign convention).
Substituting these values in equation (3), we get $\dfrac{1}{{{v_2}}} = \dfrac{1}{{ - 10}} - \dfrac{{\left( {x + 120} \right)}}{{ - 180x}}$ .
The above equation is simplified as $\dfrac{1}{{{v_2}}} = \dfrac{{ - 18x + x + 120}}{{180x}}$ .
Finally, we have ${v_2} = \dfrac{{180x}}{{120 - 17x}}$ .
This image formed at ${v_2}$ now acts as the object for refraction from the glass-air interface.
Step 4: Find the position of the image formed by the refraction at the glass-air interface.
Now, $u = {v_2} = \dfrac{{180x}}{{120 - 17x}}$ will be the position of the object and $v = - x$ will be the position of the image as the image should coincide with the position of the pin. The radius of curvature of the concave surface is $R = - 60{\text{cm}}$(by sign convention).
Then for refraction, we use the expression $\dfrac{{{\mu _a}}}{v} - \dfrac{{{\mu _g}}}{u} = \dfrac{{{\mu _a} - {\mu _g}}}{R}$ ----- (4)
Substituting for $u = \dfrac{{180x}}{{120 - 17x}}{\text{, }}v = - x{\text{, }}{\mu _g}{\text{ = 1}}{\text{.5, }}{\mu _a} = 1$ and $R = - 60$ in equation (4)
we get, $\dfrac{1}{{ - x}} - \dfrac{{1.5\left( {120 - 17x} \right)}}{{180x}} = \dfrac{{1 - 1.5}}{{ - 60}}$ .
Simplifying the above equation gives us $\dfrac{{ - 1}}{x} - \dfrac{{\left( {120 - 17x} \right)}}{{120x}} = \dfrac{1}{{120}}$
or, $\dfrac{{120 + 120 - 17x}}{{120x}} = \dfrac{{ - 1}}{{120}}$ . This equation gets reduced to $\dfrac{{120 + 120 - 17x + x}}{{120x}} = 0$ .
i.e., $240 - 16x = 0$
Solving the above equation we get, $x = \dfrac{{240}}{{16}} = 15{\text{cm}}$ .
Thus the position of the pin is placed at a distance $x = 15{\text{cm}}$ from the surface of the lens so that the image of the pin will coincide with it.
Now the concave part of the lens is filled with water. Thus the image of the pin no longer coincides with it.
Step 5: Sketch a diagram for the setup where the concave surface is filled with water. Find the position of the image formed by refraction between the water-glass interface.

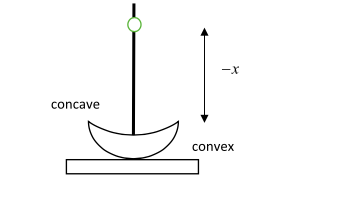
Let $u = - x'$ be the new position of the pin (object) and ${v_1}$ be the position of the image formed on refraction. The radius of curvature of the concave surface is $R = - 60{\text{cm}}$(by sign convention).
Then for refraction, we use the expression $\dfrac{{{\mu _g}}}{{{v_1}}} - \dfrac{{{\mu _w}}}{u} = \dfrac{{{\mu _g} - {\mu _w}}}{R}$ ----- (5)
Substituting for $u = - x'{\text{, }}{v_1}{\text{, }}{\mu _g}{\text{ = 1}}{\text{.5, }}{\mu _w} = \dfrac{4}{{\sqrt 3 }}$ and $R = - 60$ in equation (5)
we get, $\dfrac{{1.5}}{{{v_1}}} - \dfrac{{\dfrac{4}{3}}}{{ - x'}} = \dfrac{{1.5 - \left( {\dfrac{4}{3}} \right)}}{{ - 60}}$ .
Simplifying the above equation we have $\dfrac{{1.5}}{{{v_1}}} - \dfrac{4}{{ - 3x'}} = \dfrac{1}{{ - 360}}$
or, $120\left( {4.5x' + 4{v_1}} \right) = - {v_1}x'$ . This equation gets reduced to $540x' + 480{v_1} = - {v_1}x'$ .
Simplifying the above equation we get, ${v_1} = \dfrac{{ - 540x'}}{{\left( {x' + 480} \right)}}$ ------ (6).
Equation (6) represents the position of the image formed by refraction.
This image formed at ${v_1}$ now acts as the object for reflection by the convex surface.
Step 6: Find the position of the image formed by reflection at the silver-coated convex surface.
The silver-coated convex surface acts as a concave mirror and its focal length will be $f = \dfrac{R}{2}$ .
Now for reflection, the mirror equation is given by, $\dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{f}$ , or $\dfrac{1}{v} = \dfrac{1}{f} - \dfrac{1}{u}$ ----- (7).
Let the position of the image formed by reflection be ${v_2}$ . We have the position of the object as $u = \dfrac{{ - 540x'}}{{\left( {x' + 480} \right)}}$ and focal length will be $f = \dfrac{{ - 20}}{2} = - 10{\text{cm}}$ .
Substituting these values in equation (7), we get $\dfrac{1}{{{v_2}}} = \dfrac{1}{{ - 10}} - \dfrac{{\left( {x' + 480} \right)}}{{ - 540x'}}$ .
The above equation is simplified as $\dfrac{1}{{{v_2}}} = \dfrac{{ - 54x' + x' + 480}}{{540x'}}$ .
Finally, we have ${v_2} = \dfrac{{540x'}}{{480 - 53x'}}$ .
This image formed at ${v_2}$ acts as the object for refraction at the glass-water interface.
Step 7: Find the position of the image formed by the refraction at the glass-water interface.
Now, $u = {v_2} = \dfrac{{540x'}}{{480 - 53x'}}$ will be the position of the object and $v = - x'$ will be the position of the image as the image should coincide with the position of the pin. The radius of curvature of the concave surface is $R = - 60{\text{cm}}$(by sign convention).
Then for refraction, we use the expression $\dfrac{{{\mu _w}}}{v} - \dfrac{{{\mu _g}}}{u} = \dfrac{{{\mu _w} - {\mu _g}}}{R}$ ----- (8)
Substituting for $u = \dfrac{{540x'}}{{480 - 53x'}}{\text{, }}v = - x'{\text{, }}{\mu _g}{\text{ = 1}}{\text{.5, }}{\mu _w} = \dfrac{4}{3}$ and $R = - 60$ in equation (8)
we get, $\dfrac{1}{{ - x'}} - \dfrac{{1.5\left( {480 - 53x'} \right)}}{{540x'}} = \dfrac{{\left( {\dfrac{4}{3} - 1.5} \right)}}{{ - 60}}$ .
Simplifying the above equation gives us $\dfrac{{ - 1}}{{x'}} - \dfrac{{\left( {480 - 53x'} \right)}}{{360x'}} = \dfrac{1}{{360}}$
or, $\dfrac{{360 + 480 - 53x'}}{{360x'}} = \dfrac{{ - 1}}{{360}}$ . This equation gets reduced to $\dfrac{{360 + 480 - 53x' + x'}}{{360x'}} = 0$ .
i.e., $840 - 52x' = 0$
Solving the above equation we get, $x' = \dfrac{{840}}{{52}} = 16.15{\text{cm}}$ .
Thus the position of the pin is placed at a distance $x' = 16.15{\text{cm}}$ from the surface of the lens filled with water so that the image of the pin coincides with it.
Step 8: Calculate the distance through which the pin is moved when the concave surface is filled with water.
Initially, we found that when the pin is placed at a distance $x = 15{\text{cm}}$ the image of the pin coincides with it
When the concave surface was filled with water, the pin had to be placed at a distance $x' = 16.15{\text{cm}}$ so that its image coincides with it.
Therefore, when water is added to the concave surface, the pin must be moved through a distance $\Delta x = x' - x = 1.15{\text{cm}}$ upwards for the image of the pin to coincide with it.

Note: When representing any measure of distance, sign convention must be applied. By sign convention, the position of the object is negative for both the concave mirror and concave lens. The position of the image is negative for a concave lens but it is positive for a concave mirror. The focal length is negative for a concave mirror and concave lens.