Question

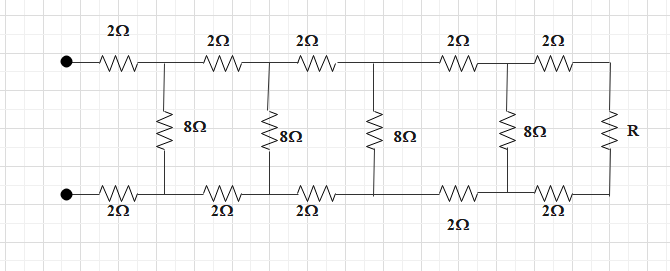
Consider a ladder network shown in figure. What should be the value off resistance R, so that effective resistance between A and B becomes independent of the number of elements in the combination?

$\begin{align}
  & \text{A}\text{. 2}\Omega \\
 & \text{B}\text{. 4}\Omega \\
 & \text{C}\text{. 8}\Omega \\
 & \text{D}\text{. 16}\Omega \\
\end{align}$

Answer 1

Hint: Obtain the expression for the total resistance of a circuit when we connect more than one resistance in series and in parallel. Observe the circuit given where we have the same resistances in every loop of the circuit and every $8\Omega $ resistance is connected in parallel to the previous loop. When we consider, every $8\Omega $ resistance is connected in parallel to the total $8\Omega $ resistance of the loop, then the total resistance is independent of the number of elements in the circuit.

Complete answer:
If we observe the circuit carefully, in every loop of the ladder network, we have two $2\Omega $ resistance connected in series with another resistance.

Now, we need to select the resistance R such that the total effective resistance between A and B will be independent of the number of elements in the combination. To do this we need to make the resistance connected in series with the two $2\Omega $ resistance in every loop equal.

When two resistances ${{R}_{1}}$ and ${{R}_{2}}$ are connected in series in a circuit, the total resistance of the circuit is given as,
$R={{R}_{1}}+{{R}_{2}}$
When two resistances ${{R}_{1}}$ and ${{R}_{2}}$ are connected in parallel to each other in a circuit, the total resistance of the circuit is given as,
$\dfrac{1}{R}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}$

Now, if we observe the above combination, the resistance of each branch is $8\Omega $ . if we consider two $2\Omega $ and one $4\Omega $ resistance connected in series, then the total resistance will be $8\Omega $. When two $8\Omega $ are connected in parallel, the total resistance will become $4\Omega $. This total $4\Omega $ resistance will be again connected in series with the previous two $2\Omega $ resistances to give a $8\Omega $ resistance. This way at the end we will always get a total of $8\Omega $ resistance which will be independent of the number of elements in the combination.
For this to happen at the last loop we need to get a $8\Omega $ resistance in parallel connection with the $8\Omega $ resistance of the previous loop. At the last branch we have two $2\Omega $ resistances connected in series with another resistance R.
We can write,

\[\begin{align}
  & ~~2\Omega +R+2\Omega =8\Omega \\
 & R=4\Omega \\
\end{align}\]

So, the value of the resistance R should be $4\Omega $.

So, the correct answer is “Option B”.

Note:
When we use a $2\Omega $, $8\Omega $ and $16\Omega $ resistance in the position of R, the value of the total resistance of the circuit changes with the number of elements in the combination i.e. the total effective resistance of the combination depends on the number of elements on the circuit.