Question

Consider the following L.P.P.
Maximize $Z = 3x + 2y$
Subject to the constraints
\[x + 2y \leqslant 10\]
\[3x + y \leqslant 15\]
\[x,y \geqslant 0\].
(a) Draw its feasible region.
(b) Find the corner points of the feasible region.
(c) Find the maximum value of Z.

Answer 1

Hint: First we will create the inequalities into equations and then draw their graphs and find the intersection points and marks the region as required and then find the value of Z on the intersection points and the corner values and choose maximum among them and thus, we have answer to all out parts as required.

Complete step-by-step answer:
We have the equations:- \[x + 2y \ le 10, 3x + y \ le 15\].
Let us change these into equalities for once to draw them on a region:-
\[x + 2y = 10, 3x + y = 15\].
Let us make table for plotting in their values:-
First for \[x + 2y = 10\]:
\[\boxed{\begin{array}{*{20}{c}}
  x&0&10 \\
  y&5&0
\end{array}}\]
Now for \[3x + y = 15\]:
\[\boxed{\begin{array}{*{20}{c}}
  x&5&0 \\
  y&0&15
\end{array}}\]
Now let us plot them on a graph as follows:
          

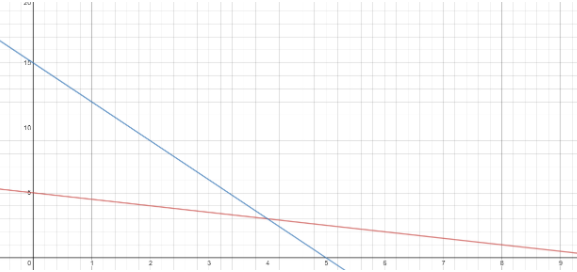
Here, the blue line represents \[3x + y = 15\] and the red line represents \[x + 2y = 10\].
We clearly see that the intersection point is (4, 3).
Now, if we consider the inequalities again we see that they are more oriented towards the origin. Therefore, their graph will give us the required feasible region.
So here is the answer of part a:
The feasible region is the region which is overlapped by both red and blue in the first quadrant only because we also have the inequalities \[{\text{ }}x,y \geqslant 0\]
               

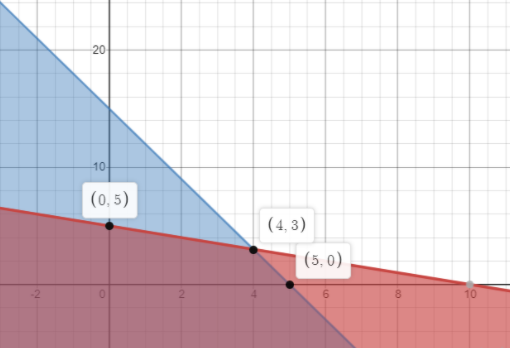
Seeing the graph, we have the answer of the part (b) as:
The corner points are (0, 5), (4, 3) and (5, 0) and (0, 0)
Now, we need to maximize Z. For that we will find the value of Z at all the corner points.
Since, we have: $Z = 3x + 2y$
Therefore, $Z{|_{(0,5)}} = 3 \times 0 + 2 \times 5 = 10$
$Z{|_{(4,3)}} = 3 \times 4 + 2 \times 3 = 18$
$Z{|_{(5,0)}} = 3 \times 5 + 2 \times 0 = 15$
$Z{|_{(0,0)}} = 3 \times 0 + 2 \times 0 = 0$.
Hence, the maximum value of Z is at (4, 3) which is 15.

So, the correct answer is “Option C”.

Additional Information: Applications of the method of linear programming were first seriously attempted in the late 1930s by the Soviet mathematician Leonid Kantorovich and by the American economist Wassily Leontief in the areas of manufacturing schedules and of economics, respectively, but their work was ignored for decades. During World War II, linear programming was used extensively to deal with transportation, scheduling, and allocation of resources subject to certain restrictions such as costs and availability.

Note: The students must remember to bring back the inequalities from the equation because using equation will definitely give us the required corner points but not the shaded region.
Sometimes, we may also forget to check the value of Z at origin which is very necessary as well.