Question

Consider the function f defined by \[f\left( x \right)=x-x\left( x \right)\] ,where $x$ is a positive variable, and \[\left( x \right)\] denotes the integral part of $x$ and show that it is discontinuous for integral values of $x$ ,and continuous for all others. Is the function periodic? If periodic, what is its period? Draw its graph.

Answer 1

Hint: We need to show that \[f\left( x \right)=x-x\left( x \right)\] is discontinuous for integral values of $x$ and continuous for all others. We have to find the continuity at a point $x=c$ such that $\displaystyle \lim_{x \to {{c}^{-}}}f(x)=\displaystyle \lim_{x \to {{c}^{+}}}f(x)=f(c)$ . By using the equation $\displaystyle \lim_{x \to {{c}^{-}}}f(x)=\displaystyle \lim_{h\to 0}f(c-h)$ for LHS and $\displaystyle \lim_{x \to {{c}^{+}}}f(x)=\displaystyle \lim_{h\to 0}f(c+h)$ for RHS , we can find the continuity of the function. Next, to plot the graph, we need to find the points. For this, we will use \[(x)=\left\{ \begin{align}
  & ... \\
 & .. \\
 & \begin{matrix}
   -1 & ; & -1\le x<0 \\
\end{matrix} \\
 & \begin{matrix}
   0 & ; & 0\le x<1 \\
\end{matrix} \\
 & \begin{matrix}
   1 & ; & 1\le x<2 \\
\end{matrix} \\
 & ... \\
 & ... \\
\end{align} \right.\] for integral value from which we can get the points for the given function by suitable substitution. From the graph, we can analyze whether the function is periodic or not.

Complete step by step answer:
We need to show that \[f\left( x \right)=x-x\left( x \right)\] is discontinuous for integral values of $x$ and continuous for all others.
Let $c$ be an integer.
$f(x)$ is continuous at $x=c$ if
$\displaystyle \lim_{x \to {{c}^{-}}}f(x)=\displaystyle \lim_{x \to {{c}^{+}}}f(x)=f(c)$
Let us first evaluate LHS
$\displaystyle \lim_{x \to {{c}^{-}}}f(x)=\displaystyle \lim_{h\to 0}f(c-h)$
Substituting for $x=c-h$ in \[f\left( x \right)=x-x\left( x \right)\] , we get
$\displaystyle \lim_{x \to {{c}^{-}}}f(x)=\displaystyle \lim_{h\to 0}(c-h)-(c-h)[c-h]$
We know that integral part of $[c-h]=(c-1)$ .
Therefore, $\displaystyle \lim_{x \to {{c}^{-}}}f(x)=\displaystyle \lim_{h\to 0}(c-h)-(c-h)(c-1)$
Applying the limit, we get
$\displaystyle \lim_{x \to {{c}^{-}}}f(x)=(c-0)-(c-0)(c-1)$
$\Rightarrow \displaystyle \lim_{x \to {{c}^{-}}}f(x)=c-c(c-1)$
On simplifying further, we get
$\displaystyle \lim_{x \to {{c}^{-}}}f(x)=c-{{c}^{2}}+c$
\[\Rightarrow \displaystyle \lim_{x \to {{c}^{-}}}f(x)=2c-{{c}^{2}}...(i)\]
Similarly, we do for RHS.
$\displaystyle \lim_{x \to {{c}^{+}}}f(x)=\displaystyle \lim_{h\to 0}f(c+h)$
Substituting the value $x=c-h$ in \[f\left( x \right)=x-x\left( x \right)\] , we get
$\displaystyle \lim_{x \to {{c}^{+}}}f(x)=\displaystyle \lim_{h\to 0}(c+h)-(c+h)[c+h]$
We know that integral part of $[c-h]=c$ .
Therefore, $\displaystyle \lim_{x \to {{c}^{+}}}f(x)=\displaystyle \lim_{h\to 0}(c+h)-(c+h)c$
Applying the limit, we get
$\displaystyle \lim_{x \to {{c}^{+}}}f(x)=(c+0)-(c+0)c$
$\Rightarrow \displaystyle \lim_{x \to {{c}^{+}}}f(x)=c-{{c}^{2}}...(ii)$
From $(i)\text{ and }(ii)$ ,
$LHS\ne RHS$
Thus, $f(x)$ is not continuous at $x=c$ .
That is, $f(x)$ is not continuous at all integral points. Hence, it will be continuous at other points.
Now let us plot the graph of \[f\left( x \right)=x-x\left( x \right)\] .
We know that \[(x)=\left\{ \begin{align}
  & ... \\
 & .. \\
 & \begin{matrix}
   -1 & ; & -1\le x<0 \\
\end{matrix} \\
 & \begin{matrix}
   0 & ; & 0\le x<1 \\
\end{matrix} \\
 & \begin{matrix}
   1 & ; & 1\le x<2 \\
\end{matrix} \\
 & ... \\
 & ... \\
\end{align} \right.\]
Therefore, \[f\left( x \right)=x-x\left( x \right)=\left\{ \begin{align}
  & ... \\
 & .. \\
 & \begin{matrix}
   x-x(-1) & ; & -1\le x<0 \\
\end{matrix} \\
 & \begin{matrix}
   x-x(0) & ; & 0\le x<1 \\
\end{matrix} \\
 & \begin{matrix}
   x-x(1) & ; & 1\le x<2 \\
\end{matrix} \\
 & ... \\
 & ... \\
\end{align} \right.\]
Solving, we get
\[f\left( x \right)=\left\{ \begin{align}
  & ... \\
 & .. \\
 & \begin{matrix}
   2x & ; & -1\le x<0 \\
\end{matrix} \\
 & \begin{matrix}
   x & ; & 0\le x<1 \\
\end{matrix} \\
 & \begin{matrix}
   0 & ; & 1\le x<2 \\
\end{matrix} \\
 & ... \\
 & ... \\
\end{align} \right.\]
Now let us plot the graph.

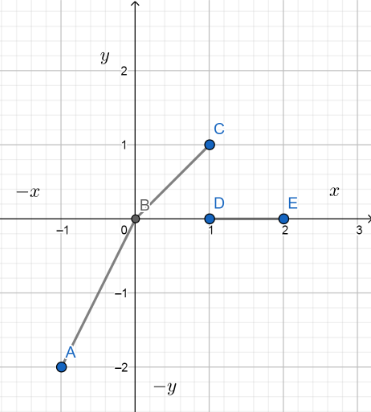
From the graph, it is clear that the function \[f\left( x \right)=x-x\left( x \right)\] is not periodic.

Note:
 Let us see what is the value of the greatest integer.
If $x=3$ then $(x)\text{ or }[x]=3$ .
If $x=6.55$ then $(x)\text{ or }[x]=6$ .
Therefore, If \[x=c\] then $(x)\text{ or }[x]=c$
If \[x={{c}^{+}}=c+h\] then $(x)\text{ or }[x]=c$
If \[x={{c}^{-}}=c-h\] then $(x)\text{ or }[x]=c-1$
 If A function $f(x)$ is continuous at $x=c$ if $\displaystyle \lim_{x \to {{c}^{-}}}f(x)=\displaystyle \lim_{x \to {{c}^{+}}}f(x)=f(c)$ . This is the main criteria of continuity. In this problem, the given function is not periodic. Periodic functions are functions that that repeats its values at regular intervals, for example, the trigonometric functions. Period of a function is distance between the repetitions of any function or it is the distance along the x-axis that the function has to travel before it starts to repeat its pattern.