Question

Construct a circle circumscribing a regular hexagon whose diameter is 6cm.

Answer 1

Hint: To construct any geometrical figure of precision, a ruler and a compass are required. A circle circumscribing a hexagon means, the hexagon is inside the circle, so we draw a circle first and then draw a hexagon in it.

Complete step-by-step answer:

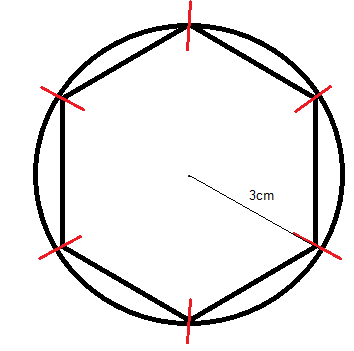
Given data, Diameter of circle = 6cm
⟹radius of circle r = $\dfrac{{\text{d}}}{2}$= 3cm.
The construction is done in a stepwise manner
Step 1: Take a ruler and measure the diameter as 6 cm.
Step 2: Using a compass, measure half a diameter (i.e. the radius) and draw the circle at the center of the radius as shown in the figure.
Now, perimeter of circle = 2πr = 2×3.14×3 = 18.84cm. So the perimeter is divided into 6 parts, $\dfrac{{18.84}}{6} = 3.14$
Step 3: From the compass measure 3.14 cm and cut the circle into 6 equal parts as shown in the figure.
Step 4: Join the arc and form a regular hexagon.
Step 6: Circles circumscribing and inscribing a regular hexagon is drawn below.

Note: In order to solve this type of question the key concept is to make the construction in a stepwise manner. Formula for the perimeter of a circle = 2πr, where r is the radius of a circle. A regular hexagon has 6 equal sides, which is why we divided the perimeter of the circle into 6 equal parts.