
Construct a cyclic quadrilateral XYZW in which WX=3.5cm,
Answer
419.4k+ views
Hint: In this question we are asked to construct a cyclic quadrilateral. For that we should be aware about the basic geometrical construction steps. We will create the quadrilateral step by step with the help of a ruler and a compass. The use of a protractor should also be known because we would need to make cuts at several spots at certain angles.
Complete step by step answer:
A cyclic quadrilateral is a quadrilateral which has all its four vertices lying on a circle. It is also sometimes called inscribed quadrilateral. The circle which consists of all the vertices of any polygon on its circumference is known as the circum-circle or circumscribed circle.
First, draw a line segment WX which has length 3.5cm. After that pointing from X, make an angle of
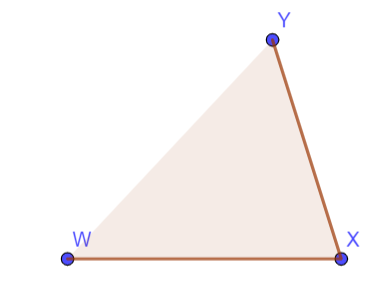
Now, draw the perpendicular bisector of XY and WX. The bisectors of XY and WX will meet at a new point O.

Now, taking O as the centre, draw a circle of radius OX. Now, construct the angular bisector of
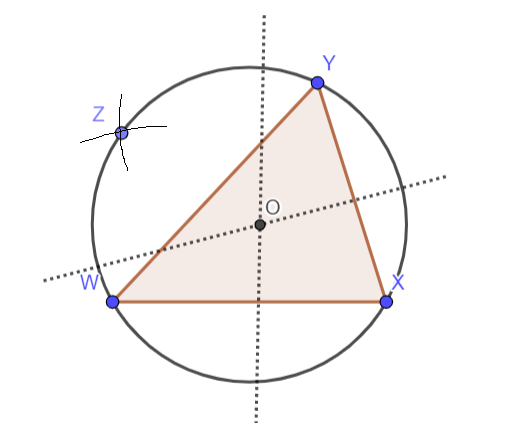
Lastly, join the points W,X,Y and Z. This quadrilateral constructed would be the required quadrilateral.
The constructed diagram looks like follows:
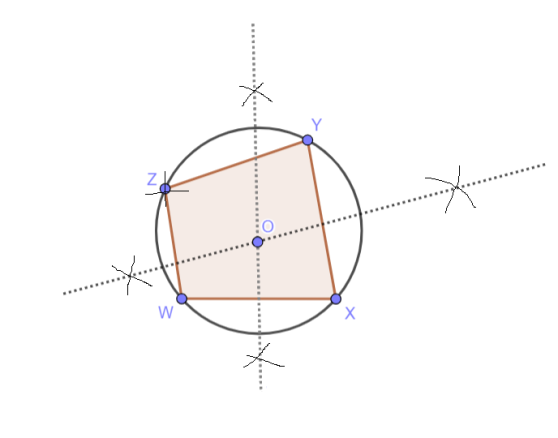
Note: While constructing the quadrilateral, make sure that you take the accurate distance whenever you are making a mark or identifying a new point on the plane. Also, you should be aware about the use of a protractor, make sure that you mark the angle at the correct spot otherwise that would lead to an invalid figure.
Complete step by step answer:
A cyclic quadrilateral is a quadrilateral which has all its four vertices lying on a circle. It is also sometimes called inscribed quadrilateral. The circle which consists of all the vertices of any polygon on its circumference is known as the circum-circle or circumscribed circle.
First, draw a line segment WX which has length 3.5cm. After that pointing from X, make an angle of

Now, draw the perpendicular bisector of XY and WX. The bisectors of XY and WX will meet at a new point O.

Now, taking O as the centre, draw a circle of radius OX. Now, construct the angular bisector of

Lastly, join the points W,X,Y and Z. This quadrilateral constructed would be the required quadrilateral.
The constructed diagram looks like follows:

Note: While constructing the quadrilateral, make sure that you take the accurate distance whenever you are making a mark or identifying a new point on the plane. Also, you should be aware about the use of a protractor, make sure that you mark the angle at the correct spot otherwise that would lead to an invalid figure.
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Where did Netaji set up the INA headquarters A Yangon class 10 social studies CBSE

What are the public facilities provided by the government? Also explain each facility

SI unit of electrical energy is A Joule B Kilowatt class 10 physics CBSE

The capital of British India was transferred from Calcutta class 10 social science CBSE

Identify the phrase s in the following sentence The class 10 english CBSE

How fast is 60 miles per hour in kilometres per ho class 10 maths CBSE




