Question

Construct a quadrilateral BLUE in which \[{\rm{BL}} = 7{\rm{cm, LU}} = 6{\rm{cm, UE}} = 3.5{\rm{cm, BE}} = 5.5{\rm{cm and }}\angle {\rm{B = 7}}{{\rm{0}}^0}\]

Answer 1

Hint:
Here, we have to construct a quadrilateral with the help of straight lines. Firstly we have to draw a straight line of given length BL and then from the end B we will draw a line of an angle of\[{\rm{7}}{{\rm{0}}^0}\]. Then, we have to mark an arc of length BE on the inclined line of\[{\rm{7}}{{\rm{0}}^0}\] and that point is E. Then from the point E and from the point L we will draw an arc which will intersect each other and give the point U. Then by joining all the points we will be able to draw the quadrilateral BLUE.

Complete step by step solution:
It is given that the lengths and angle of the quadrilateral BLUE is
\[{\rm{BL}} = 7{\rm{cm, LU}} = 6{\rm{cm, UE}} = 3.5{\rm{cm, BE}} = 5.5{\rm{cm and }}\angle {\rm{B = 7}}{{\rm{0}}^0}\]
So firstly we have to draw a line of 7 cm length and name it as side BL

Now we have to draw an inclined line of angle\[{\rm{7}}{{\rm{0}}^0}\] form the point B as angle given at B is \[{\rm{7}}{{\rm{0}}^0}\] and after drawing this inclined line we have to mark an arc of length 5.5 cm on it as it is given that\[{\rm{BE}} = 5.5{\rm{cm}}\] and the intersection point is named as point E.

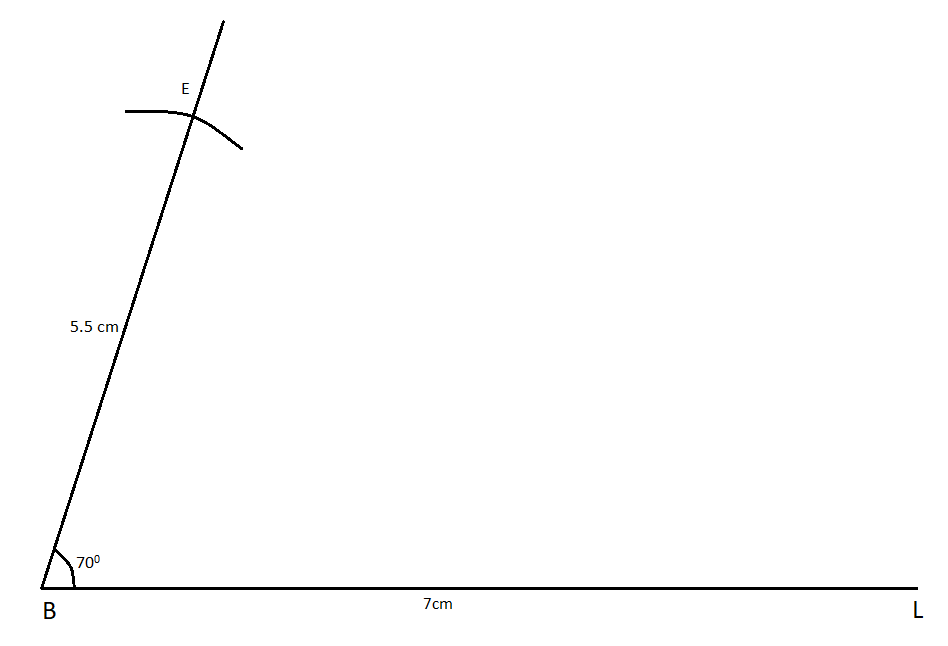
Now from the point E and L, we have to draw arcs using the bisector to obtain the point U. Now draw an arc of length 3.5 cm taking E as the center and draw an arc of length 6 cm taking L as the center and cutting the other arc. Point of intersection obtained is point U. Then join the points EU and LU with a straight line.

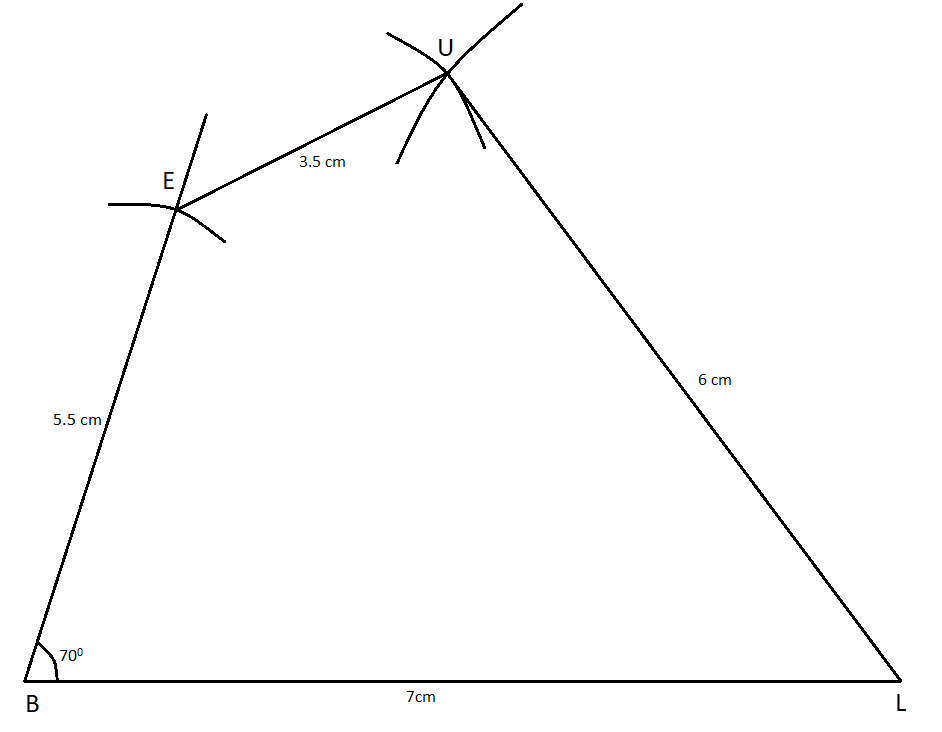
Hence, the required quadrilateral BLUE is drawn.

Note:
Geometry is the branch of mathematics that deals with points, lines and shapes. In geometry, bisection is the division of something into two equal parts. Bisection is generally done with a line which is called a bisector. There are two main types of bisectors i.e. line segment bisector and angle bisector.
A line segment bisector is a line or line segment that divides the line into two equal parts or which passes through the midpoint of the line segment.
Angle bisector is the line or line segment that divides an angle into two equal parts. An angle has only one bisector. Also there are two types of angle bisectors i.e. interior and exterior angle bisector.