
Construct a triangle with sides 5 cm, 6 cm and 7 cm and then another triangle whose sides are
Answer
519.6k+ views
Hint: First of all we will construct a triangle, say
Complete step-by-step answer:
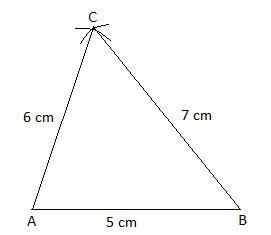
We have been given the sides, 5 cm, 6 cm and 7 cm.
Let us suppose the triangle to be
Now we will have to follow the following steps to draw
a. We will draw a base of side 5 cm.
b. With A as center and 6 cm as radius, draw an arc.
c. With B as center and 7 cm as radius, draw an arc.
d. Let C be the point where two arcs intersect. Now join AC and BC.
Thus,
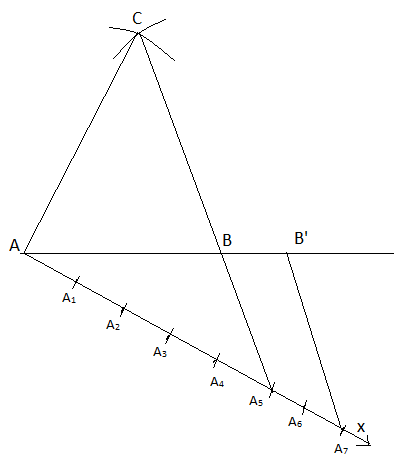
Now, let’s make a similar triangle with scale factor
We will follow the following steps to make the similar triangle:
a. Draw any ray AX which makes an acute angle with AB.
b. Now we will mark 7 points
c. We will join
d. Now draw a line through B’ parallel to the line BC to intersect AC extended at C’. Thus
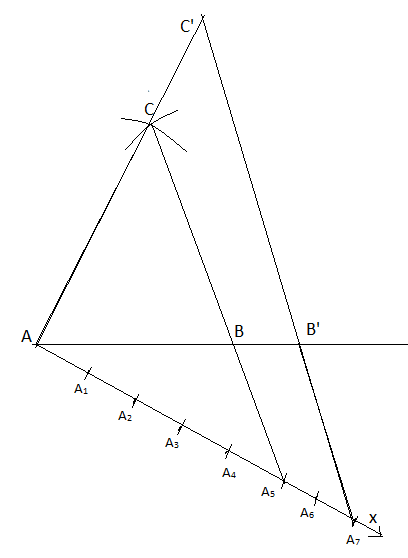
Note: Be careful while taking the points of the ray AX, they should be equidistant at each other. Also, remember that the number of points on the ray is equal to that number which is greater between the numerator and denominator of the scale factor.
Complete step-by-step answer:
We have been given the sides, 5 cm, 6 cm and 7 cm.
Let us suppose the triangle to be
Now we will have to follow the following steps to draw
a. We will draw a base of side 5 cm.
b. With A as center and 6 cm as radius, draw an arc.
c. With B as center and 7 cm as radius, draw an arc.
d. Let C be the point where two arcs intersect. Now join AC and BC.
Thus,

Now, let’s make a similar triangle with scale factor
We will follow the following steps to make the similar triangle:
a. Draw any ray AX which makes an acute angle with AB.
b. Now we will mark 7 points
c. We will join

d. Now draw a line through B’ parallel to the line BC to intersect AC extended at C’. Thus

Note: Be careful while taking the points of the ray AX, they should be equidistant at each other. Also, remember that the number of points on the ray is equal to that number which is greater between the numerator and denominator of the scale factor.
Latest Vedantu courses for you
Grade 10 | CBSE | SCHOOL | English
Vedantu 10 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹37,300 per year
Recently Updated Pages
Master Class 4 Maths: Engaging Questions & Answers for Success

Master Class 4 English: Engaging Questions & Answers for Success

Master Class 4 Science: Engaging Questions & Answers for Success

Class 4 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Trending doubts
What does R mean in math class 7 maths CBSE

How many crores make 10 million class 7 maths CBSE

Convert 200 Million dollars in rupees class 7 maths CBSE

What were the major teachings of Baba Guru Nanak class 7 social science CBSE

Which of the following is not the function of Municipal class 7 social science CBSE

Write down a pair of integers whose sum is 0-class-7-maths-CBSE





