Question

Construct an equilateral triangle of side \[6cm\] and mark the incircle.

Answer 1

Hint: We have to first construct an equilateral triangle and then mark the incircle. We will require a scale/ruler, protractor and rounder in order to draw the diagram. We can draw the triangle directly with the help of scale or use the compass and draw it with the help of arc.

Complete step by step solution:
We will follow the following steps to draw the diagram:
1) Draw \[\vartriangle ABC\] such that \[AB = BC = AC = 6cm\] with the help of a ruler and protractor.
The measure of the angles will be \[\angle A = \angle B = \angle C = {60^ \circ }\].
We can also construct the triangle with help of arc as follows:
2) Draw a line segment \[BC = 6cm\].

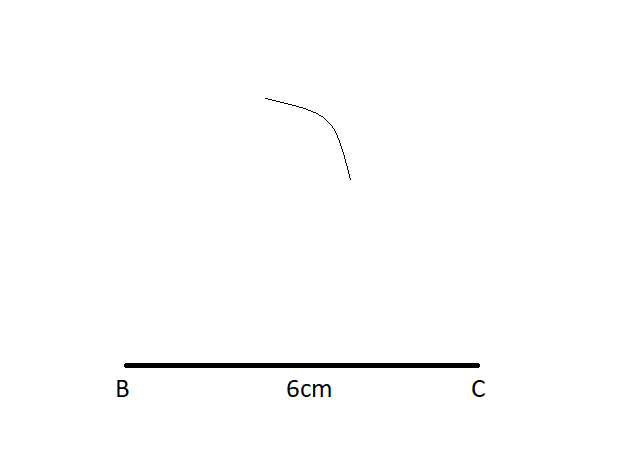
3) Now draw an arc from the centre point \[B\] taking radius as \[6cm\] on its right side as follows-

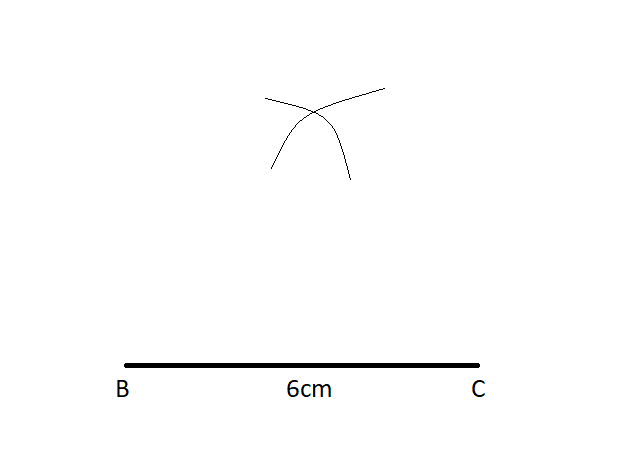
3) Similarly, draw an arc from the centre point \[C\] taking radius as \[6cm\] on its left side such that it intersects with previous arc as follows-

4) Join the point of intersection at point \[A\] and join the point \[B\] and \[C\] with it which will give us \[AB = BC = AC = 6cm\]-

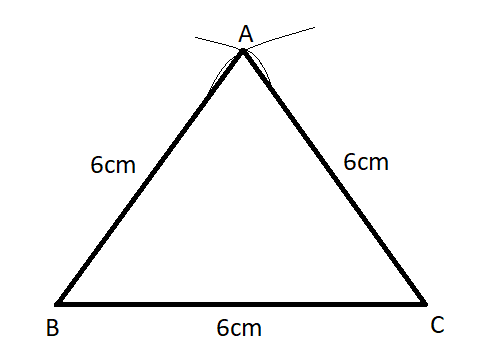
Hence, we have constructed an equilateral triangle \[\vartriangle ABC\].
5) Now in order to draw the incircle, we have to draw angle bisectors of all three angles. We draw arcs from \[\angle A\],\[\angle B\] and \[\angle C\] intersecting at point \[O\] as follows:
6) Now we draw a circle with centre \[O\] touching all the sides of triangle as follows:

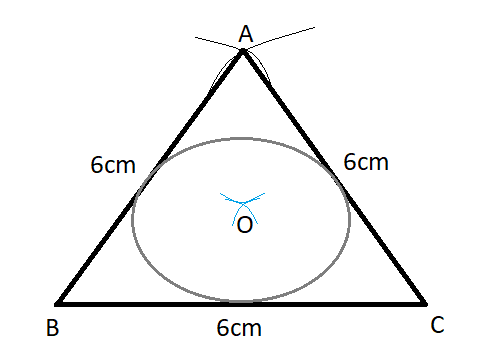
Here, their circle will be incircle since it’s touching all the three sides of the triangle. Centre \[O\] is the marking point of the incircle.

Note:
Equilateral triangle is the one which has all its three sides equal. All the three angles of the equilateral triangle will measure \[{60^ \circ }\]. Incircle means the circle inscribed in the triangle or any other shape so as to touch each side.