Question

Construct the incircle of the equilateral triangle whose one side is 8cm.

Answer 1

Hint: For an equilateral triangle circumcenter, orthocenter, centroid and incentre coincide and incircle touches the sides of the triangle at the foot of medians, altitudes, angular bisectors, perpendicular bisectors of the sides.

Complete step-by-step answer:

Construction of incircle:
1.Draw the equilateral triangle ABC of side 8 cm.

2. Now plot the centre of each side (D, E and F) and construct the medians( these medians will act as altitudes, angular bisectors, perpendicular bisectors of the sides).

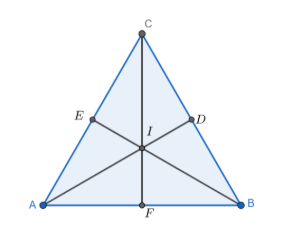
3. We know incentre coincides with the centroid of triangle I, and the incircle touches the triangle at the foot of medians .
4. Now draw the circle with centroid I as the center and the foot of medians the points on incircle where incircle touches the sides.

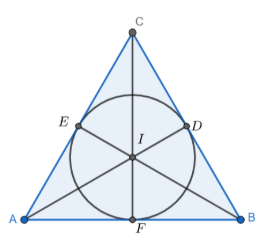
Hence, an incircle is constructed.

Note: We can calculate the centre using the following method.
As we know in the equilateral triangle circumcenter and the incenter coincides. So, the point of concurrency of the perpendicular bisectors gives us the circumcenter which is also the incentre in this case.
Now draw the circle with the obtained centre with the radius r.
Where r is defined as the in radius or radius of incircle. The radius of incircle is given by:
radius of incircle=\[\dfrac{abc}{4\Delta }\]
Where a, b, c are the sides of the triangle and \[\Delta \] is the area of the triangle. Here a=b=c and \[\Rightarrow r=\dfrac{2a}{\sqrt{3}}\]
\[\Rightarrow r=\dfrac{2a}{\sqrt{3}}\]
Therefore, the radius of the incircle is \[\dfrac{2a}{\sqrt{3}}\].