
How do you convert 73 degrees to radians?
Answer
468.3k+ views
Hint: Here in this question, we have to convert degrees into radians. We should know that 360 degrees =
Let’s solve the question now.
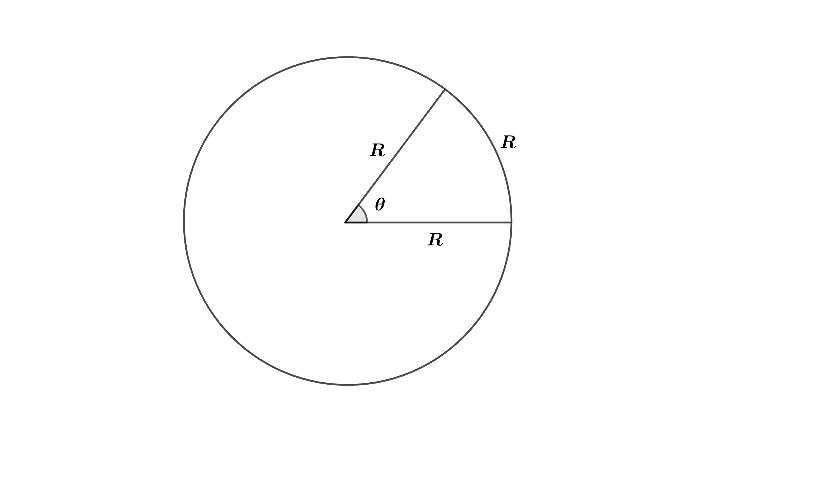
Let us make a circle and assume ‘R’ as a radius of a circle and draw the arc of the same length ‘R’. When an angle
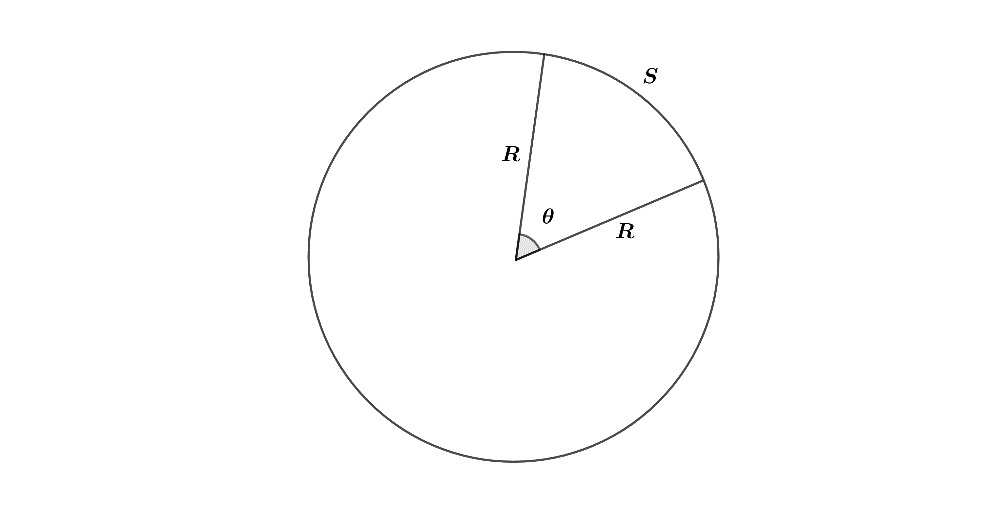
From the above figure, if we wish to find
One Revolution of a circle is equal to
Now if
After reducing the terms, we will get:
This is the conversion which we will be using to convert degrees to radians.
If we wish to convert any degree into radian, we have to multiply the degree with a factor of
First, multiply 73 with
Now, take
The next step is to multiply 73 with 3.14, we will get:
Now, after dividing the value in radians will be:
So this is our final answer.
Note:
There is an alternative method for this question. As we know that degrees and radians are based on equality i.e.
Now we have to solve for ‘x’. We will cross multiply:
Next is to keep ‘x’ alone and take all the terms to the other side. We get:
Put x = 3.14, we get:
On solving further we will get:
On dividing, we get:
Let’s solve the question now.
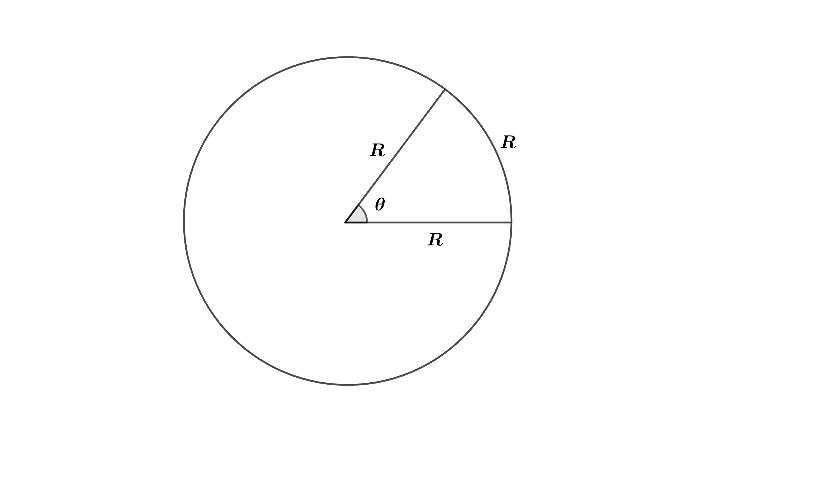
Let us make a circle and assume ‘R’ as a radius of a circle and draw the arc of the same length ‘R’. When an angle

From the above figure, if we wish to find
One Revolution of a circle is equal to
Now if
After reducing the terms, we will get:
This is the conversion which we will be using to convert degrees to radians.
If we wish to convert any degree into radian, we have to multiply the degree with a factor of
First, multiply 73 with
Now, take
The next step is to multiply 73 with 3.14, we will get:
Now, after dividing the value in radians will be:
So this is our final answer.
Note:
There is an alternative method for this question. As we know that degrees and radians are based on equality i.e.
Now we have to solve for ‘x’. We will cross multiply:
Next is to keep ‘x’ alone and take all the terms to the other side. We get:
Put x = 3.14, we get:
On solving further we will get:
On dividing, we get:
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Write the following in Roman numerals 25819 class 7 maths CBSE

Trending doubts
Where did Netaji set up the INA headquarters A Yangon class 10 social studies CBSE

A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What are the public facilities provided by the government? Also explain each facility




