Question

‌Coordinates‌ ‌of‌ ‌the‌ ‌vertices‌ ‌of‌ ‌a‌ ‌quadrilateral‌ ‌are‌ ‌\[(2,‌ ‌-‌ ‌1),(0,2),(2,3)\]‌ ‌and‌ ‌\[(4,0)\]‌ ‌.‌ ‌The‌ ‌angle‌ ‌between‌ ‌its‌ ‌diagonals‌ ‌will‌ ‌be‌ ‌
1.\[{90^‌\circ‌ ‌}\]‌ ‌
2.\[{0^‌\circ‌ ‌}\]‌ ‌
3.\[{\tan‌‌^{‌ ‌-‌ ‌1}}(2)\]‌ ‌
4.\[{\tan‌^{‌ ‌-‌ ‌1}}\left(‌ ‌{\dfrac{1}{2}}‌ ‌\right)\]‌

Answer 1

Hint: In the question we are given the vertices of a quadrilateral and we are required to find the angle between its diagonals. In order to find this we will first try to identify the quadrilateral. Different types of quadrilaterals are square, rectangle, rhombus, trapezium, parallelogram. We will do so by finding the slopes of the respective lines and constructing the diagram for the same. Once we get the slopes of lines we can use the formula \[\tan \theta = \dfrac{{{m_2} - {m_1}}}{{1 + {m_1}{m_2}}}\] where \[\theta \] is the angle between the diagonals.

Complete step-by-step solution:
Construct the diagram of quadrilateral using the given information.

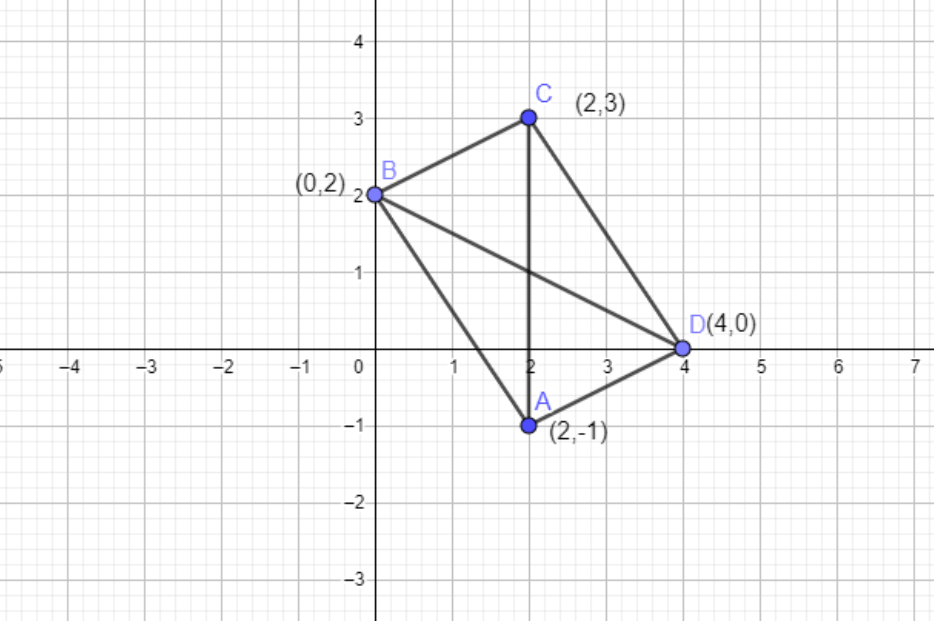
The points \[(2, - 1),(0,2),(2,3)\] and \[(4,0)\] are the coordinates of the vertices of the quadrilateral.
Let us assume the points \[A(2, - 1),B(0,2),C(2,3)\] AND \[D(4,0)\].
Be the vertices.
Now let us find the slopes .
Slope of AB \[ = \dfrac{{2 + 1}}{{0 - 2}} = - \dfrac{3}{2}\]
Slope of BC \[ = \dfrac{{3 - 2}}{{2 - 0}} = \dfrac{1}{2}\]
Slope of CD \[ = \dfrac{{0 - 3}}{{4 - 2}} = - \dfrac{3}{2}\]
Slope of DA \[ = \dfrac{{ - 1 - 0}}{{2 - 4}} = \dfrac{1}{2}\]
Since slopes of AB and CD are equal , hence they are parallel to each other.
Since slopes of BC and DA are equal , hence they are parallel to each other.
HENCE THE GIVEN POINTS ARE VERTICES OF A PARALLELOGRAM.
Now let us find the angle between the diagonals AC and BD .
Let \[{m_1}\] and \[{m_2}\] be the slopes of AC and BD respectively.
\[{m_1} = \dfrac{{3 + 1}}{{2 - 2}} = \infty \]
And \[{m_2} = \dfrac{{0 - 2}}{{4 - 0}} = - \dfrac{1}{2}\]
We know that \[\tan \theta = \dfrac{{{m_2} - {m_1}}}{{1 + {m_1}{m_2}}}\] where \[\theta \] is the angle between the diagonals.
\[\tan \theta = \dfrac{{ - \dfrac{1}{2} - \infty }}{{1 + \infty \left( { - \dfrac{1}{2}} \right)}}\]
        \[ = \infty \]
Therefore we get \[\theta = {\tan ^{ - 1}}\infty = {90^ \circ }\]
Therefore option (1) is the correct answer.

Note: Although a quadrilateral always has four sides, four angles, and four vertices, the measure of the sides and angles differ. It is to be noted that the sum of the interior angles of a quadrilateral is always equal to \[{360^ \circ }\]. For solving such problems we should know the different types of quadrilateral and their differences and after finding which particular type of quadrilateral we have, we use its properties.